Figure 1. UTM Grid
Dr. Dean S. Hartley III
Hartley Consulting
Dr. Andrew Loebl
Oak Ridge National Laboratory
Mr. Brian Rigdon, Mr. Brian P. van Leeuwen
Sandia National Laboratory
Contribution from
Dr. Raymond Harrigan
Sandia National Laboratory, Retired
The focus of this paper is the study and example of problems brought on by the lack of commonality determination or its exploitation in battle command.
We draw examples from operational Army systems and from military simulations. These examples lead us to forecast problems that can be experienced in the creation of the UA System of Systems (SoS).
In 1999, the Mars Lander crashed. Engineers on the ground calculated the size of the rocket-firing using feet-per-second of thrust, a value based on the English measure of feet and inches. However, the spacecraft computer interpreted the instructions in Newtons-per-second, a metric measure of thrust. The difference was 1.3 meters a second and the lander entered the atmosphere at a lower point than planned for -- and crashed.1 This was a failure of commonality.
Space programs are not the only programs vulnerable to commonality failures. There is the, probably apocryphal, story of the artilleryman who didn't use the common function for computing his gun lay and ended landing his round precisely in the post commander's back yard. Probabilities of kill are used in military calculations; however, there are many varieties of probabilities of kill: total probability of kill, Single Shot Probability of Kill (SSPK), SSPK as the probability of kill given a shot, SSPK as the probability of kill given a hit, SSPK for the first shot, SSPK for subsequent shots, etc. Assuming a common definition is being used is dangerous. Opportunities for failures of commonality in military operations are boundless.
1.1. Background of the work
This document describes recent work by the FCS Integrated Support Team (FIST) under the Unit of Action (UA) Program, SMART Director. The UA is an implementation of the Army's Future Combat System (FCS). The FIST was formed and organized to address critical technical and analytical challenges that had been identified throughout the earlier Concept Exploration phases of the UA program. One purpose of the FIST Commonality Pathfinder Project has been to determine the impact of problems caused by insufficient exploitation of commonality and to advise on corrective measures.2
1.2. Organization of the paper
We begin in Section 2 with a discussion of the general nature of computers and their problems compounded, in certain ways and circumstances, with commonality that would not be experienced by humans, using map reading as an example. This discussion sets the stage for examining the problems that can and do occur when commonality exploitation is inadequate.
Section 3 provides an extended discussion of how precise instructions about each specific computer function can ensure linking between/among functions, but may not be sufficient to truly integrate the functions. Again, a map example is used.
In Section 4, we discuss several different examples of commonality problems and their effects on simulations. In Section 5, we show that commonality problems are equally significant in real-world operational systems, today.
The UA SoS will involve both simulations and more conventional computer systems. Section 6 describes the need for commonality involving modeling and simulation for the SoS. Section 7 describes concerns of the need for commonality within the general computer systems of the SoS.
The final section recaps the lessons that need to be applied to the UA SoS with regard to commonality. An appendix is provided to restate the definitions that were introduced in this paper.
Some human processes may be directly implemented in computers. For example, the logic of bookkeeping processes of accounting requires the posting of numbers to appropriate accounts, and categories within. The act of posting a number to a ledger can be converted directly to the entry of the number in the corresponding data table by a computer, provided the database of resources available to that device includes proper cross-reference information.
Other human processes require significant cataloging and often changes in order to convert them to computer processes. Map reading provides an example.
A human has to be taught to properly orient the map in a number of ways, e.g., to orient to the terrain to understand the correspondence of the paper representation to what the student sees and understands before him. The human has to be taught to understand the significance of the various symbols on the map, how to calculate distances represented between features, how to create diagrams to represent the slopes between points of interest, and numerous other basic methods and tools for gathering information implied by the symbols and scaled, representative features of the paper to ground truth. To actually use a particular map -- to read it, the human has to be taught, usually by experience, how to decide what is important and what is not for a particular application. When the soldier is presented with an OPORD that contains map overlays, there is an implied function ReadMap(Overlayi).
A computer executing a process which might be identified as ReadMap(Overlayi) would require successful implementation of an array of properly sequenced task instructions that allows the device to serially address, completely, the full set of tasks and sort out, admittedly at very high speeds, the action(s) stipulated and if successful, then digitally interface results of that explicit sorting and transmit the desired results to the intended user/use, even assuming all input is in appropriate digital form and scale, etc. Certainly the detailed set of instructions that convert into the equivalent, but not necessarily identical, suite of functions that correspond to the human training mentioned above would be developed, and for many many instances of such tasks, acceptable instructions have been developed and/or software coding shortcuts implemented in COTS materials. However, developing and implementing that instruction set would be necessary, but not sufficient to implement ReadMap(Overlayi) regardless of how complete that instruction set might be (or become). Ultimately the accomplishments of that computer sorting would confront the need of that product to be employed in a decision in real world application. Without the logic and capability for decision making in conditional and unconditional situations, each sort by the computer would, in non-purposeful coordination, require a goal for each execution of the function, e.g., determine the minimum distance between Red force units and Blue force units or determine where line of sight exists from a given point.
Thus, for a human, ReadMap(Overlayi) would be a function with syntactical commonality (and the same output in all cases -- "understanding"), it would not exhibit commonality at the functional level for UA action. For FCS/UA device processing, more parameters would be required and each set of parameters must imply the determined, dependent results. Understanding cannot be duplicated in a computational environment and the unique abilities and logic of human beings to draw understanding from sorting of information is not yet available from any other device.
The inescapable issue for the UA and FCS in the strategic and foreseeable future is ensuring that the powerful technologies now associated with integrated computer systems, ubiquitous network-centric environments, astounding abilities to detect and classify signals from the environment in analog form and convert that to digital input, be optimized. That, if successfully and meticulously complete, will free humans to do what they, and only they, do best: Effect understanding, formulate alternatives to a goal, comprehend the results of actions tactically and strategically, and make decisions-sometimes simultaneous with other decisions and with, largely, inadequate data.
Humans can and usually do execute actions as a result of decision making that does not possess strict commonality of input data streams. In order for machine systems to function at their promised effect and efficiency, the lineage, validation, pedigree, authority, proper transference, and unanimity in computational expression must be precise, reportable, resistant to entropy, and digitally available to all other processes as required. Strict commonality among digital systems within a system of systems is only recently, technologically possible, in practical terms, to the systems or system of systems of the warfighter/commander. This is an attribute of the new paradigm in C4ISR for which the performance enhancements envisioned for FCS may be enabled.
Encapsulation or data-hiding is a powerful component of object oriented programming. The idea is to protect the internal operations of a code module from inadvertent tampering by external code. A non-exhaustive example will be helpful in describing the benefits and problems with this concept.
The designers of a project have determined that the computation of the distance between two points will be performed frequently and that a code module should be written to perform this function. Before coding the function, they determine the interface: the code should accept data on two locations, each defined by a decimal latitude value, a decimal longitude value, and a height in meters above sea level; the code should produce a distance in meters. The designers pass this information to the coders with instructions that the code must have this exact interface, should protect the internal variables against external corruption, should run very quickly, and must be correct. The designers have also passed these requirements to those who will be coding the calls to the distance function and are satisfied that they have specified their needs completely, because any code meeting these requirements will link correctly (interoperate) with any code needing the distance results.
The coders are satisfied with the requirements, also. They will make all of the internal variables private, so that if they use "x" as a variable they don't have to worry that some other module will (inappropriately) also use "x" as a variable. The data hiding or encapsulation provided will ensure, for example, that the computer doesn't think the two "x" variables are the same variable, which would allow an external module to change the value of the internal variable in the middle of an operation, resulting in invalid results. The coders also know that if they can make the code more efficient using some other data representations, e.g., feet for meters, they are free to do that, so long as the output conforms to the specification.
At this point in the example, the benefits of encapsulation are clear. Modules can be written independently, without concerns about variable naming. This approach reduces the need for cross-communication among teams, which was a major time consumer and source of errors in the days of FORTRAN programming.
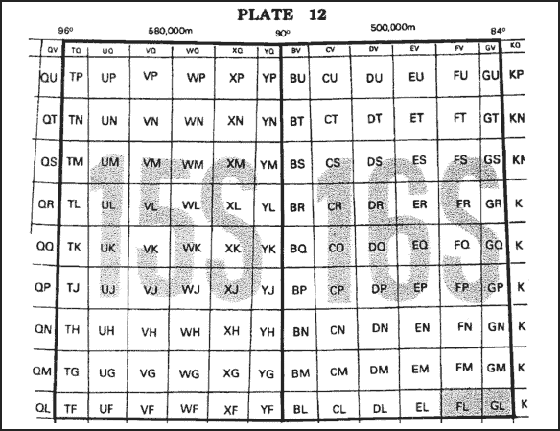
In this example, the coders have worked on Army models for many years and are familiar with Army Universal Transverse Mercator (UTM) grid maps.3 As shown in Figure 1, the Earth is divided into grid zones. Each grid zone is divided into 100,000 meter grid squares (the smaller boxes). A point is labeled with "northing" and "easting" coordinates, representing meters (or multiples thereof, depending on the scale) north and east of the reference point.
The coders know that given two points in a grid square, the distance between them can be calculated as the square root of the sum of the squared difference of northings and the squared difference of eastings. They are accustomed to artillery ranges being contained in a 100 kilometer square and assume that all interesting distances are similar. The coders then proceed to convert the input latitudes and longitudes into grid coordinates. The differences in elevations are handled as yet a third Euclidean dimension in determining the distance, which is output.

Figure 1. UTM Grid
At this point, the problems of encapsulation become clear. The fact that the coders are using a Euclidean geometry model of the Earth is unknown to the users of the distance function. This function will yield correct values for small distances, for which the curvature of the Earth is insignificant; however, it will not yield correct values for continental-scale distances.
Further, other distance functions exist that are of importance in military decision making. For example, while tactical advances may use cross-country movement, most military movement uses the road network. A distance function that delivers the shortest distance from one point to another on the road network would be valuable and would require the same interface. This road-distance function would require data on the road network. However, the designers might have assumed that that is common data, not required in the interface. A second road-distance function is important, and would restrict the routing to those roads of sufficient quality to carry a particular set of vehicles. Such a road-distance function would more properly include the characteristics of the set of vehicles in the interface.
One physical example for the difference between linking and interoperability is the plug for an electrical appliance and the socket that provides the electricity. The appliance can link to the electrical system if the plug fits into the socket. Linkage says nothing about the interoperability of the resulting linkage. For example, the voltage required may or may not be the same as that supplied and the cycles per second required may or may not be the same as that supplied.
So long as the plug fits, the two can link. Anyone who has bought plug adapters (see "interface" above) for foreign use, without also using the appropriate converter, will have learned that linking is not the same as interoperating. Note that an interface can create linkage without creating interoperability or (if it has the correct functionality) an interface can create interoperability. In some cases, however, the differences are so great that an interface cannot be created to support interoperability.
When discussing linkage in the domain of software functions, a simple example is syntactic correlation versus semantic correlation. The "interface" (unfortunately this word is used in multiple ways; here it means the definition of the inputs and outputs of a software module) of a function defines the number, types, and (frequently) the sequence of the inputs to the function and the type of the output. Type is a programming construct that may be understood to differentiate between integer, number containing decimal fractions, and other more arcane objects.
For example, if one function presents its output as numbers in an alphanumeric format, e.g., "1" or "12," and the second function requires its input to be formatted as integers, an interface (call it T) that translates text numbers to integers would enable the two functions to link. However, if the output of the first function has English units and the input of the second function is assumed to be metric units, some incompatibility remains. The function T is an interface; however, it is not a fully successful interface in this case. What is required is an interface, TC, that translates and converts from English to metric units.
Use of functions that have proper linking does not guarantee that integration (interoperability) will be achieved, because integration includes the presumption of mutually compatible models within the modules being integrated.
This section includes five examples. Four of the examples relate to combat simulations, three from the training domain and one from analysis. The final example relates to simulating robot actions, similar to expected needs for the FCS UA.
4.1. Validity
In general, the validity of any military simulation is unknown. The Military Operations Research Society (MORS) developed the following definitions, which were adopted by the Department of Defense (DODI 5000.61):
Even given the restriction that the validity of a model is based on its intended uses, rather than some absolute standard, most military models are so complex and have so many possible branches that even exercising all of the possibilities is impossible. Also, modern military models are data driven, meaning that part of the overall model of reality is contained in the set of data used in any given (computer) model run. Further, for many of the situations, the correct (real world) answer is unknown. For these reasons, verification and validation are discussed as processes and it is accepted that the processes will only be partially accomplished for any given model and set of uses. This is the reason for adding "accreditation." Accreditation is the effort of will, belief and faith that says this amount of verification and validation is good enough.
4.2. Validation: Commonality between a Model and Reality
The old Simulation Network (SIMNET) created a common virtual reality among the people training in Abrams tank or Bradley fighting vehicle simulators. A validation study found some problems with the trajectory functions of the early SIMNET.4 As will be seen, there is a clear difference between the trajectory function of the model and the real world trajectory function. Because, there was no direct connection between the real world and the model, the question of the time had to do with the degree of accuracy that was needed for the intended uses of the model. Here we will be more interested in what could go wrong if this lack of commonality between functions were perpetuated in the FCS, where the model and the real world will be in intimate contact.
Figure 2 depicts a Bradley firing its main gun directly away from the viewer toward a distant point (seen between the treads, under the hull). The trajectory is represented by the vertical dashed and dotted lines as it rises and then falls to the distant point. The model trajectory function agrees with the real world function in this case.
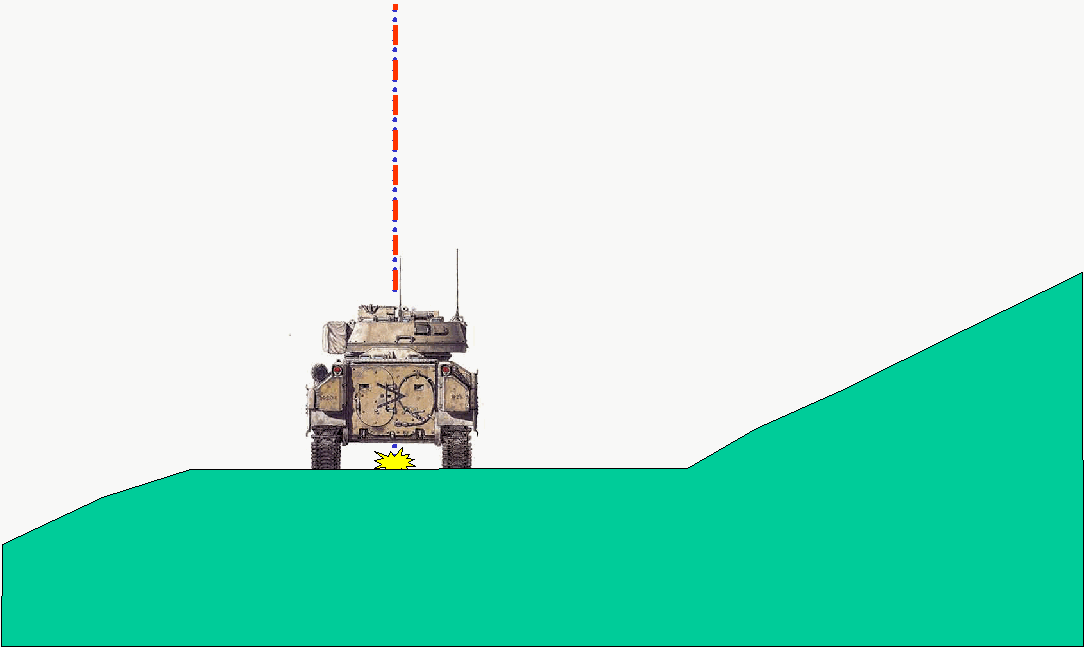
Figure 2. Real or SIMNET Bradley firing
Figure 3 illustrates the model's trajectory when the Bradley is tilted to one side by the terrain, but still aiming at a distant point directly away from the viewer. The model simply rotates the trajectory so that it is perpendicular to the ground, irrespective of gravity. In the model, the round hits the aim point.
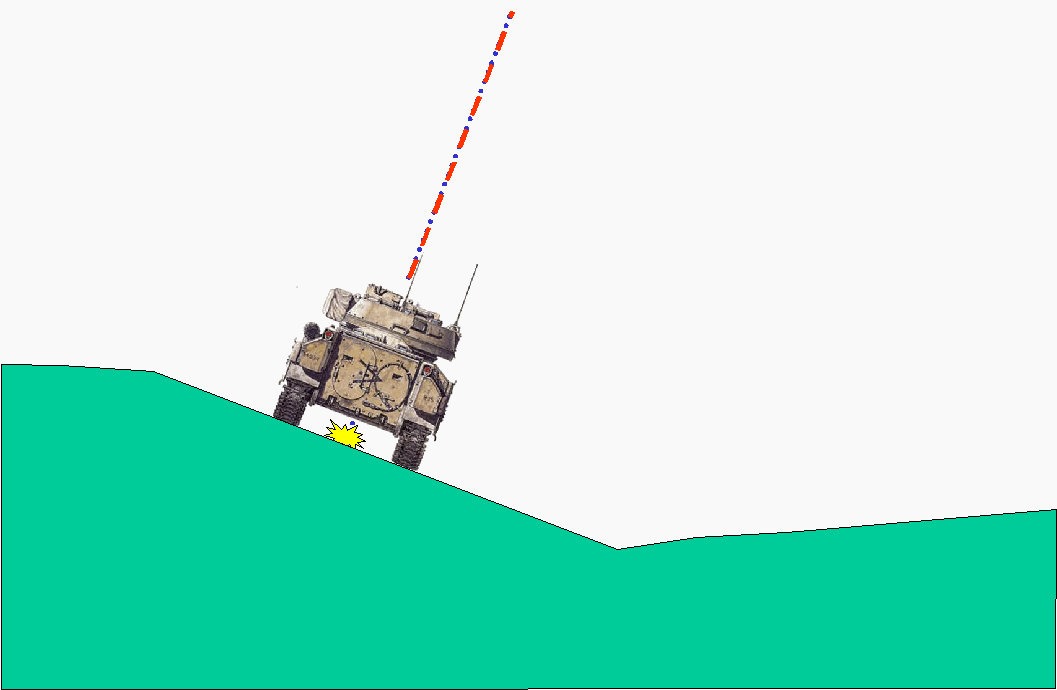
Figure 3. SIMNET Bradley firing on a cant
Figure 4 illustrates the current problem. Suppose there is a real UAV flying through the apex of the model's trajectory as the round passes through that point.
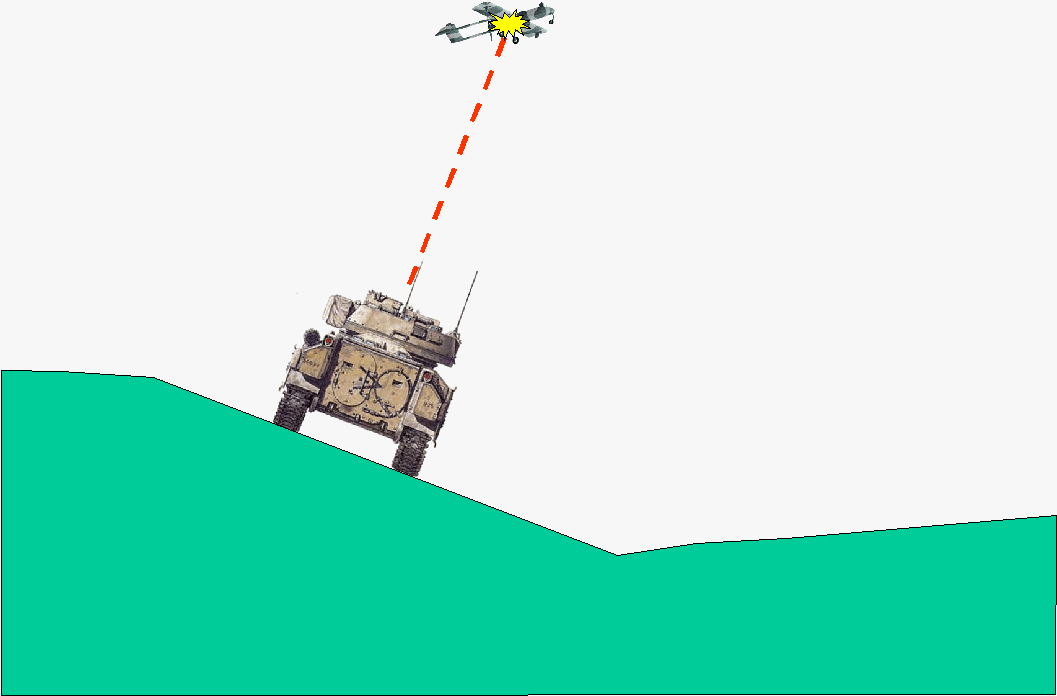
Figure 4. SIMNET Bradley firing on a cant, with obstacle
The required connection between virtual simulations and live training must generate a simulated hit on the UAV, despite the fact that the real world trajectory for the desired aim point would not intersect the UAV, as shown in Figure 5. In the real world, the gunner would have to rotate the turret slightly in the uphill direction to account for the forces of gravity.
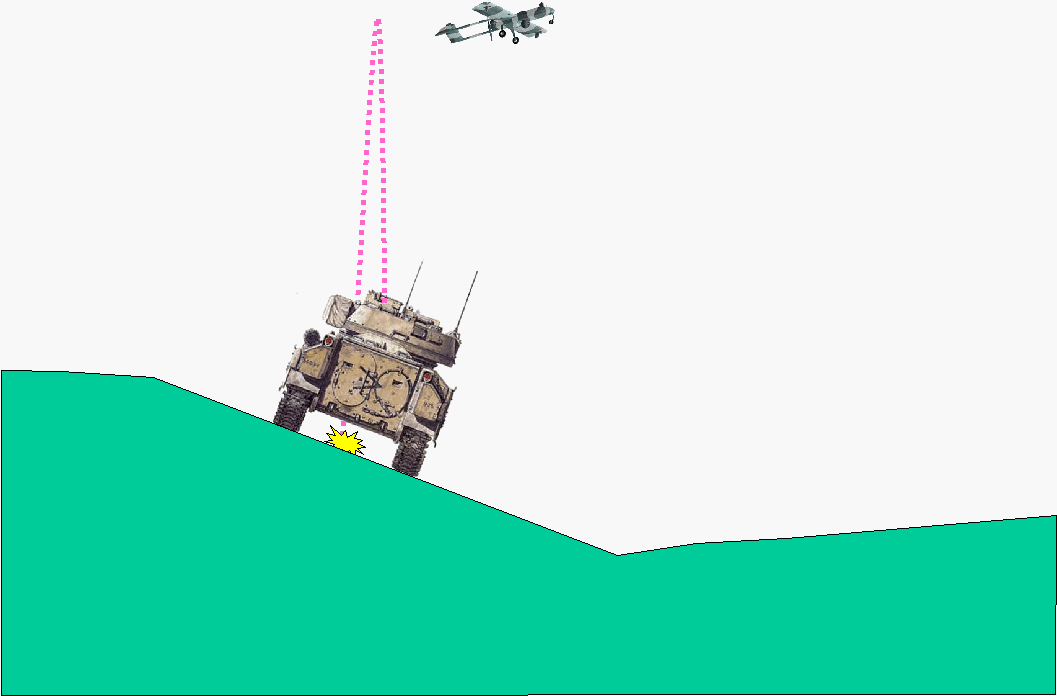
Figure 5. Real Bradley firing on a cant, with obstacle
In this case, the strictures of validation coincide with the desirability of commonality. The model's trajectory may or may not have been accurate enough for the use in the original SIMNET; however, it certainly would not be accurate enough in the situation illustrated here. A rigorous search for potentially common functions would have highlighted these two functions (model trajectory and real trajectory) as potentially common functions.
4.3. Simple Commonality Example
When SIMNET was first introduced, the following situation could and did occur.
1. Each vehicle calculates its own position, based on the operator's controls (speed, heading, etc.) [locationfunction1]. At times the vehicle broadcasts its position on the network, using Protocol Data Units (PDUs, formatted blocks of data).
2. Each vehicle receives PDUs and decides whether to use them (based on distance, type information in PDU, etc.). For location PDUs from other vehicles within possible viewing distance, the receiving vehicle calculates the proper view (size, orientation & position within viewing block) to display to the vehicle occupants.
3. The occupants may desire to fire a weapon at the pictured vehicle. They use the displayed location to align their weapon. The firing vehicle calculates the trajectory of the round and send PDUs containing the trajectory out on the network.
4. If the pictured vehicle is stationary and remains so, its location is correctly represented and proper firing will include the trajectory intersecting the pictured target.
5. Other vehicles, including the targeted vehicle receive the trajectory PDUs and determine whether their vehicle is hit by the round, based on their vehicle size and location [using locationfunction1]. If a vehicle determines it has been hit, it determines how much damage was done (based on round type and hit location) and broadcasts a PDU containing this information. Thus, all vehicles within sight of the hit vehicle will display a burning vehicle (if that is the indicated result of the hit).
6. Unfortunately, when network traffic is high, PDUs can be dropped, resulting in jerky motion as a vehicle is pictured as staying still until a new PDU refreshes the image. As a result, a second position calculation is performed. Because location PDUs include both location and velocity vector, receiving vehicles picture other vehicles at the location produced by adding their last velocity vector, integrated over time, to their last reported position [deadreckoning=locationfunction2].

Figure 6. SIMNET target acquired
7. Thus, if the targeted vehicle changes its velocity vector, but that PDU is lost, all other vehicles that missed that PDU, including the firing vehicle, will show the targeted vehicle at the wrong location until a new location PDU is received.
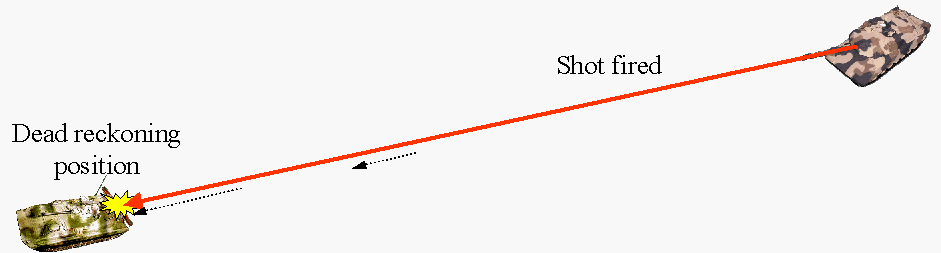
Figure 7. "Hitting" target
8. In this situation, the firing vehicle can see its round hitting the targeted vehicle and be told (by receiving no "I'm hit" PDU) that they missed the target.
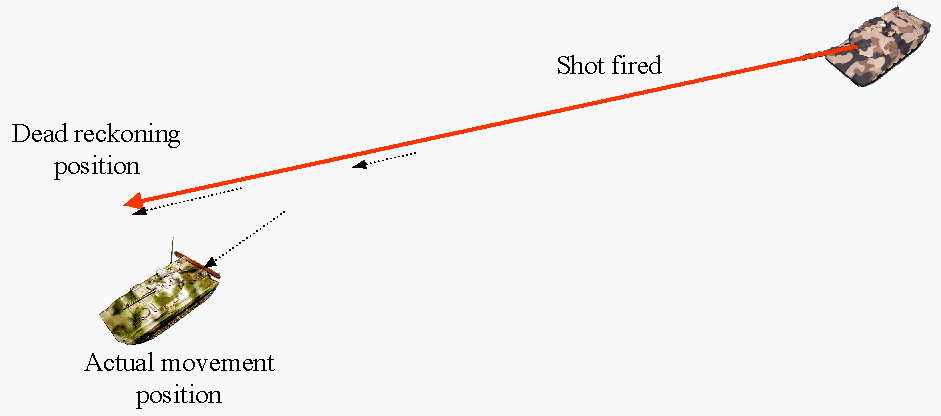
Figure 8. Real situation
This is the agreed upon sequence of events and prevents logical problems within the computers. However, if it occurs frequently enough, negative training will be the result. In the early days of SIMNET, this was not a frequent occurrence and was thus not a problem.
On the other hand, it clearly illustrates that having two different functions that perform the same task (determine the location of the targeted vehicle) can cause problems in a system. The extent and impact of the problems will, naturally, depend on the situation.
4.4. Complex Commonality Example
Military simulations are generally very complex models with very serious purposes; however, the paragraphs in the Simple Commonality Examples section above are equally relevant for complex models and simple models. The following example will make this clear.
The following situation actually occurred (during work on the Korean Battle Simulation Center5). Three military models were involved, CBS, RESA, and AWSIM. The point to be made in this example is independent of the actual validity of any of the three. The point is that it is possible for three completely valid models to be linked in mechanically flawless fashion and have the resulting system be clearly invalid.
We will discuss the example using the names of the actual models; however, we will actually be using idealized versions of the models to make the point. The idealized versions are assumed to be completely valid for their intended uses.
CBS is a land warfare simulation, which was developed by the Army to model its units and their activities in combat. Hence it models the many types of helicopters in the Army inventory. CBS models attrition to its combat vehicles as a two-step process:
probability of kill = probability of hit * probability of kill given a hit.
Perhaps the rationale was that damaged vehicles had a fair probability of being recovered and refurbished for reuse in land warfare.
RESA is a naval warfare simulation, which was developed by the Navy to model its units and their activities in combat. Hence it models the many types of helicopters in the Navy inventory. RESA models attrition to its combat vehicles as a one-step process: probability of kill is an input variable. Perhaps the rationale was that damaged vehicles had a fair probability of being lost in the sea.
AWSIM is an air warfare simulation, which was developed by the Air Force to model its units and their activities in combat. Hence it models the many types of helicopters in the Air Force inventory. AWSIM models attrition to its combat vehicles as a one-step process: probability of kill is an input variable. Perhaps the rationale was that damaged vehicles had a fair probability of being lost over land not controlled by the Air Force.
The Aggregate Level Simulation Protocol (ALSP) was the glue to link these models together. It was the predecessor to the High Level Architecture (HLA) which all current models must (by DOD standard) either support or justify non-support. It was built to use some of the conventions developed in the Simulation Network (SIMNET) world of joint viewpoint simulators. In particular, in SIMNET if one simulator fired a weapon at another simulator, the firing simulator calculated the trajectory of the round and sent packets of information containing that trajectory. The other simulators received the information and determined if their position coincided with the trajectory at the proper time, and thus they were hit, and, if so, what damage was incurred. ALSP applied this philosophy to the connection of its simulations. Thus, if an entity in one simulation fired at an entity in another simulation, the simulation of the firing entity calculated the parameters of firing and the simulation of the target entity calculated the result. If both the firer and the target were in the same simulation, that simulation did all the calculations. Because the simulations in the domain of ALSP were aggregated simulations and did not calculate trajectories, the information passed was more in the nature of, "I just shot weapon W at your entity E and hit it." We will assume, for this discussion, that ALSP performs perfectly, as designed.
As it turned out, there was at least one helicopter type that was in the inventory of the Army, the Navy, and the Air Force. The differences in the versions were small enough that the flight characteristics and vulnerabilities to weapons were identical in so far as these simulations should be concerned.
Obviously, the lack of commonality of representations causes problems in the confederation or system of simulations.
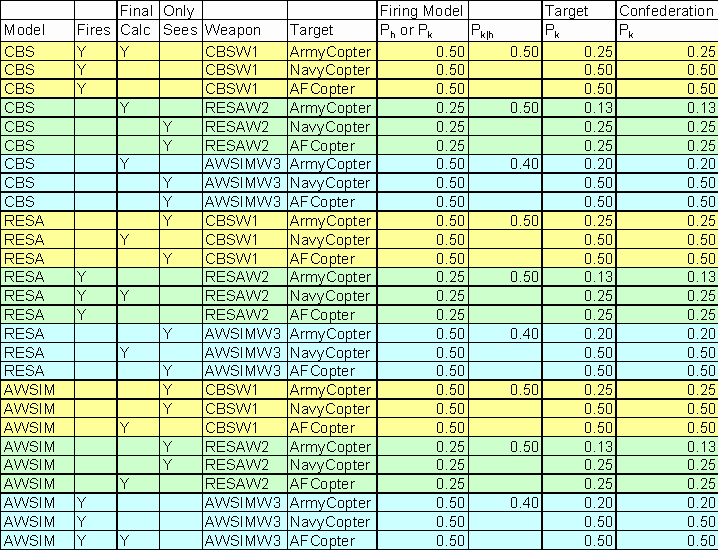
Table 1. Data Entry and Results for Attrition
In Table 1 three helicopters, all of the same type, are targeted by one weapon from each simulation. The helicopters are named for the simulation of which they are entities. The probabilities in the table are all notional and do not represent actual values.

Note that the result is that CBS helicopters are less vulnerable to all weapons than are the other equivalent helicopters -- because of the lack of commonality of representation, not because of any flaws in any of the simulations or of the ALSP. Table 2 reduces the data in Table 1 to the bare facts: if a model hits a helicopter that is originated by the Navy or the Air Force model, the helicopter dies. This is shown graphically in Figure 9. If the helicopter is originated by the Army model, it may live. It would appear that this inconsistent result could be repaired by artificially increasing the vulnerability of the ArmyCopter to all weapons in CBS, RESA and AWSIM; however, then ArmyCopter would not have the proper vulnerability with respect to other Army helicopters in CBS.
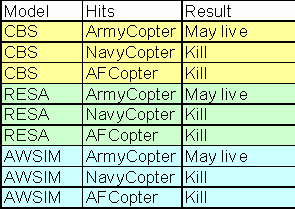
Table 2. Short Answer
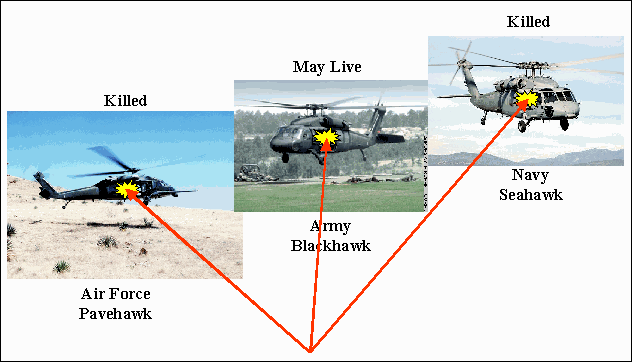
Figure 9. One type, 3 models, 2 results
From the chart, it would appear a simple matter to make selective modifications in the RESA and AWSIM probability of kill values. For example, if RESA said that its Pk value for NavyCopter and AFCopter was 0.25, but the value for ArmyCopter was 0.50. Then the Confederation Pk value in all three cases would be 0.25. Unfortunately, when RESA targets the helicopter, all it sees is a type such as "H-60." RESA can tell which helicopters it owns because it has to compute the kill; however, RESA cannot distinguish between a CBS-owned "H-60" and an AWSIM-owned "H-60." Thus, RESA only has one choice for Pk value for foreign helicopters. If it uses 0.25, the result will be correct for AWSIM helicopters and incorrect for CBS helicopters. If it uses 0.50, the results will be reversed. The inconsistency cannot be resolved in this manner because there are three simulations, not just two.
This example is a simplification. In the actual case, the only solution that would yield consistent results was to nullify the entire CBS two stage attrition process for all weapons and target pairs by setting all Ph|k values to 1.0 and using the Pk values of AWSIM and RESA. Unfortunately, this would have done violence to other parts of the CBS algorithms. As a result, helicopters were excluded from the entity sharing process to prevent any interactions among the simulations with helicopters -- a different problem of validity.
4.5. Aggregation Affects Commonality
Early models could not handle large numbers of objects, as they were constrained by computer memory and run-time. As a result, modelers used aggregates (e.g., division, battalion, company, platoon) to simulate large-scale battles. Consequently, the Army built a family of loosely-coupled or uncoupled models (e.g., Janus, CASTFOREM, VIC) to gain insights from lower-level models that were used in running higher-level models. Results from the higher-level models then motivated further research on lower-level models.
More recently, the military has pursued direct connection among models using the same level of aggregation (e.g., CBS, AWSIM, RESA), which work fairly well together. However, problems occur in connecting models using different levels of aggregation. For example, model "HighLevel" uses company-level aggregation (e.g., 8 tanks, 8 Bradley Fighting Vehicles (BFVs)) and tabulates battle losses on each side. However, model "LowLevel" uses a non-aggregated level of vehicles, which are assigned to specific units (e.g., platoon), and which fight as vehicle against vehicle with corresponding damage (e.g., mobility loss, firepower loss, vehicle kill).
HighLevel executes quickly at low resolution; however, at critical points (e.g., battle engagement of Company A) the high resolution of LowLevel could produce more believable results if the two were connected. For example, disaggregating HighLevel data results in 4 tanks each in Platoons 1 and 2, plus 4 BFVs each in Platoons 3 and 4. Moreover, the single location of Company A must be converted into 16 locations for the vehicles (e.g., via a topographically-based template). The result of this disaggregating is shown in Figure 10.
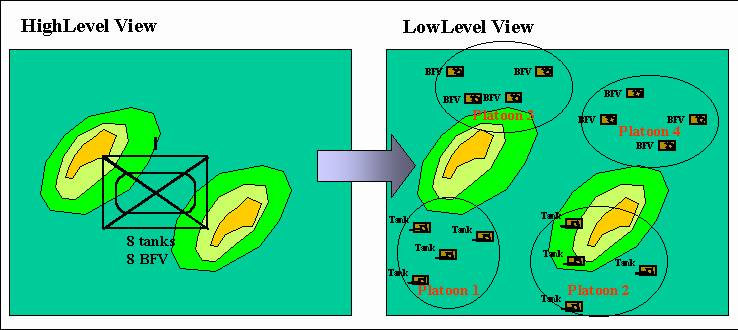
Figure 10. Disaggregation before battle
Next, LowLevel simulates the battle, which results in the loss of all 4 BFVs in Platoon 3. The re-aggregated information for HighLevel is that Company A now has 8 tanks and 4 BFVs at some new (average) location (Figure 11).
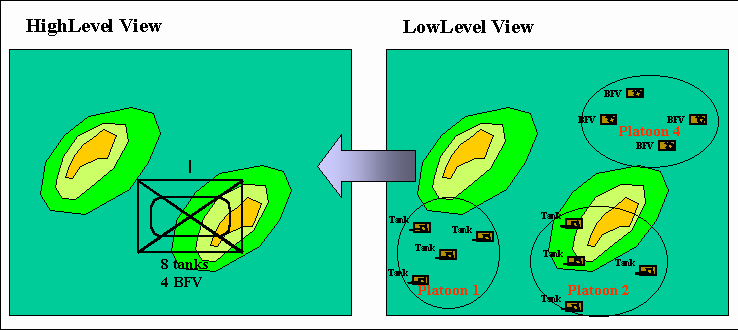
Figure 11. Reaggregation after the battle
HighLevel continues its simulation to another critical point for Company A. While Platoons 1 and 2 are disaggregated as before, the disaggregation algorithm results in each of Platoons 3 and 4 having 2 BFVs. This disaggregation is different from the previous disaggregated situation for Company A, resulting (for example) in a very different battle outcome by LowLevel, as compared to what would have happened in the previous situation where Platoon 4 had 4 BFVs and Platoon 3 had been completely lost.
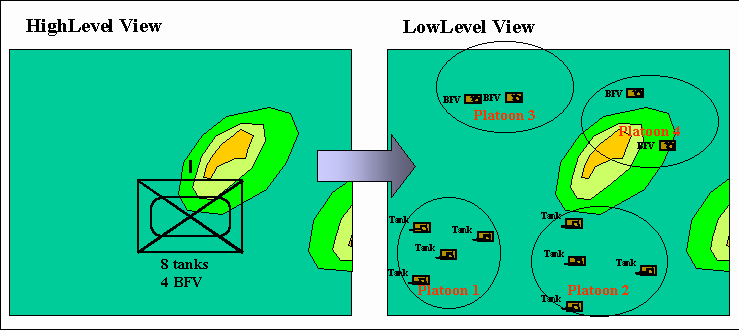
Figure 12. Second disaggregation
The disaggregation algorithm determines the particular results in these examples. In these cases, the algorithm is such that a company is assumed to have four platoons of types determined by the type of the company. The total resources are divided equally into the platoons, based on the type of resources each type of platoon is allowed. An alternative algorithm could be designed that allocates the resources up to full strength for a platoon before beginning on the next platoon. The alternative algorithm would yield correct results for this example; however, different examples could be easily constructed that would yield failures for the alternative example. The problem is that HighLevel does not carry with it the information that would permit any algorithm to recreate the disaggregated situation. Adding this information would slow the execution of HighLevel, reducing its value as a rapidly executing model.
A second problem with multiple aggregation levels is fractional units. For example, if HighLevel had 3 BFV at some point, the allocation between two platoons in LowLevel would result in 1.5 BFVs in each, which LowLevel does not allow. The problem of fractional units could also originate in HighLevel, which allows fractional losses in its higher-level simulation. For example, suppose Company-A now has 5.3 tanks and 2.7 BFVs after a combined engagement with the 2nd Brigade, which lost 8 tanks and 4 BFVs among 3 companies. LowLevel converts fractional values to the next lower integer (e.g., 5.3 to 5), performs the simulation, determines no losses, and returns 5 tanks and 2 BFVs. Upon re-aggregation into HighLevel, it appears that 0.3 tanks and 0.7 BFVs were lost, when in fact no losses occurred.
Military modelers have not resolved this aggregation/disaggregation problem, which is rooted in lack of commonality. The two models do not have common representations of the world and so cannot have direct commonality of their functions.
In both this example and the complex example above, having successfully linked systems, the developers must ensure that the linked systems interoperate. If the commonality has not been formally determined and has not been properly exploited, no interface function can make the linked systems interoperate, SOSCOE not excluded. Without the proper interface function(s), the choices are to either: compromise the intended uses, not link, or create a non-systems problem.
4.6. Swarm Robotics as Commonality Demonstration
The previous section illustrates the problems of lack of commonality in simulations. Next we describe an instance in which commonality between the simulation and the real world insured valid results. In 2000, the Intelligent Systems and Robotics Center at Sandia National Laboratories (SNL) studied robotic vehicles. A purpose of the study was to ensure an even distribution of the robots throughout a one-level building and to maintain an ad-hoc network of roving sentries.6, 7 The robots would have on-board radios and establish a token-ring network. The robots (Figure 13) were modeled prior to construction via a separate simulation (Figure 14) of the radios, sensors, controller, drive motors, chassis, and building geometry.

Figure 13. Robots
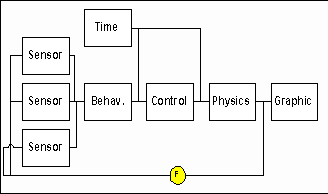
Figure 14. Robot simulation
One robot was a stationary base station; the other robots maneuvered through the building. If a robotic node lost communication, it would (a) reverse until communication was restored, (b) park, and (c) become a stationary relay. Ultrasonic sensors on each of each vehicle's four sides allowed detection of walls, obstacles, and corners, which the control unit avoided via appropriate maneuvers. The simulation included interactions among robots and their environment, as an accurate representation of their system-of-systems behavior.
The simulation showed several important emergent8 behaviors. First, an inadequate number of robots could not cover the entire building with the line-of-sight radio communications. Second, too many robots overwhelmed the communications network. Third, the initial placement of the robots strongly affected the final network topology, which was also sensitive to the building geometry via the radio performance.
While all of these results are reasonable and not unexpected, a fourth behavior was unexpected. Namely, the simulated robot jittered while negotiating a corner. This behavior initially was dismissed as a simulation anomaly, but also appeared in the physical robots as an artifact of the control interaction with the drive mechanism. As the sensor detected wall loss at a corner, the skid-steer drive would turn immediately. The turn resulted in re-detection of the wall, so the robot would go straight, again resulting in the sensor losing the wall. This behavior (turn, straight, turn, straight, etc.) caused the jitter in both the real and virtual systems. Experiments with the physical robots confirmed all of these simulation behaviors.
The control algorithms were developed by the same design teams for the real and simulation systems. The simulation had a modular structure that matched the physical systems. The results showed that the simulation accurately modeled the system-of-systems interactions of the robot swarm. This example illustrates the importance of commonality enforcement across real and simulating systems.
We have demonstrated that the lack of commonality of various kinds can cause critical flaws in simulations. While, the final example in the section on simulation commonality began to enter the real world, the main point had to do with a simulation. In this section we address the question of whether the lack of commonality can cause problems in real world operations.
5.1. Center for Army Lessons Learned
Table 3 presents examples from the Field Artillery portion of lessons learned posted on the Center for Army Lessons Learned (CALL) web site. Analysis of the reports shows that most of the problems can be attributed to lack of commonality among current systems. In this table a rough categorization of Field Artillery lessons learned has been undertaken. The three broadest areas are commonality, integration and training. Within these areas, the result-type of the problems are described as one of the following:
The column following the result-type contains a brief description of the type of system or the named system(s) that were involved in the problem. The final column gives the problem name in the CALL site.
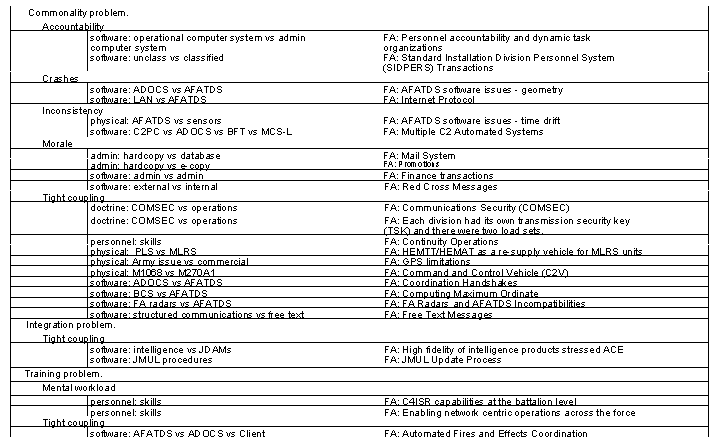
Table 3. Field Artillery Lessons Learned from Operation Iraqi
Freedom
The lack of commonality may be expressed as training problems, integration problems, or more plainly as preventable mis-matches among systems that are assumed to be able to at least properly link. The 'systems' can be software, hardware, procedural, or combinations of these. The result of the lack of determination and exploitation of commonality attributes for the purposes of these systems includes: system crashes, loss of accountability, inconsistencies, increase in mental workload, loss of morale, and reduced system performance due to loosened system coupling because human actions must be added between machine activities instead of the machine doing its own work. In each case, one or more functions that have an intended commonality are not expressed as common functions. The individual systems perform as designed; they may even be viewed as integrated; however, this lack of recognition and use of commonality determination leads to the observed disconnect in the lessons learned.
Lack of commonality exploitation in real systems causes problems today. The problems discussed in Table 3 may have been fixed by now. However, we have no doubt that there are many more that have not yet been recognized or fixed. It can be argued that these problems are arising because each of the systems was built without conscious regard for the others - that they are stove-pipes - and that the FCS UA SoS will be different. Current indications, cited as examples in other papers of this pathfinder project, are that the sheer size of the FCS is already leading to internal stove-piping. There is no reason to expect that FCS development will avoid commonality problems unless there is a conscious effort made to identify and exploit all commonality opportunities.
Further, and importantly, the examples relevant to current forces give an indication that even current force systems can be addressed to determine and exploit common functions and thus spiral-out improvements that would result in a better integrated and performing system(s) of the current and near term future force. The CALL and AAR resources of the Army could be data-of-opportunity for analysis that would, without confounding current force efforts or goals, be of practical benefit.
5.2. Non-Interoperability of S/MIME from Lack of Commonality
This example describes a case in which a standards lab defined a standard and created a standards compliance test to prevent interoperability issues. Several producers independently developed products using the defined specification. The products were built to the standard and tested to meet the standard. The result was a number of products that met the standard but were not interoperable. In many of these cases, the implementations did not have interoperability issues when working in a system comprised of a commonly produced implementation. However, issues arose when implementations from different producers were used. This occurred under conditions of very strict standards and testing definitions.
The S/MIME (Secure/Multipurpose Internet Mail Extensions) is a protocol for secure electronic mail, including digital signature, encryption, authentication, non-repudiation, message integrity, and message privacy. RSA Labs rigorously tested the implementations and awarded the seal of "S/MIME Enabled" for compliance to the standard. However, the specification allowed multiple implementations, because key interoperability features were not well-defined. It was concluded that there are a number of characteristics or properties that affect the interoperability of a given S/MIME application with other S/MIME applications. The result was several commercial "S/MIME Enabled" products that were not interoperable.9 This problem could be eliminated if commonality were required, meaning that the same instantiation MUST be used wherever needed.
If you arrived here using a keyword shortcut, you may use your browser's "back" key to return to the keyword distribution page.
Return to Hartley's Projects Page