Hartley Consulting supplies operational and economic analyses.  It also supplies project planning, organizational advice and web design.

RCIG is a small business created by Dr. John D. G. Rather in Oak Ridge, TN, to foster innovation in physics and engineering.

MAGLEV 2000 was formed to develop and commercialize the revolutionary inventions of Dr. James Powell and Dr. Gordon Danby, who invented superconducting magnetic levitation vehicles.

One result has been the creation of Sisyphus Energy, Inc., with John Rather as President and CEO and Dean Hartley as Vice President and COO.

BACKGROUND

We do not use electrical energy at a constant rate throughout the day and the electrical energy being supplied by the power grid must equal the amount being used. Because it is more cost-effective to produce energy at a constant rate, we would like to store energy during off-peak hours for use during peak usage.  Currently, we are not able to do this in meaningful quantities.

Figure 1 on the right, developed from data supplied by the U.S. Energy Information Agency (2011) and the International Energy Agency (2010), shows the average U.S. energy consumption/production by source and time of day (both Summer and Winter averages). The baseline is a production level between the low point and the high point of demand. For this data, it is about 400 gigawatts of energy.

As shown in Figure 1, nuclear power represents a about 20% of baseline use. Hydropower (from dams) and renewable sources (wind, solar, etc.) represent small fractions. Coal represents about 50%. And natural gas supplies a small part of the baseline needs. Nuclear power and coal are relatively inflexible sources. A nuclear reactor needs to run at a constant temperature, producing a constant output. Older coal-fired power plants have the same requirement.  They can be shut down; however, this is not something that can be done to adjust for hourly demand changes. Some newer coal-fired power plants can reduce output by changing the physical combustion point in boilers; however, this has only minor impact on power output.  Dams can spill water, rather than running it through the generators, and can reduce flow rates; however, they also have constraints on water level behind the dam and flow rates below the dam and depend on rainfall levels. These factors mean that additional changes to meet varying hourly demand levels are not popular with the operators. Renewable power depends on weather and cannot be used for variable demand adjustments.  Natural gas turbine plants are capable of adjusting to hourly, daily and seasonal demands and are the main source of such adjustments. However, shutting down any generating capacity represents a waste of the capital used in creating the generating capacity. The section of the figure labeled "Wasted baseline" represents generating capacity that is not used because the demand is too low. The cumulative gigawatt hours of power represented by this section comprises the most obvious opportunity for better operating the energy supply. If this available energy is captured and stored, then it can be used during the peak hours, reducing the need for the total capacity during those hours - whether natural gas or coal. Additions to the nuclear supply can reduce the need for greenhouse gas producing power plants; however, this increases the proportion of very inflexible energy generation. Having an energy storage solution remedies this potential problem.
 

Figure 1. Hourly Energy Consumption/Production

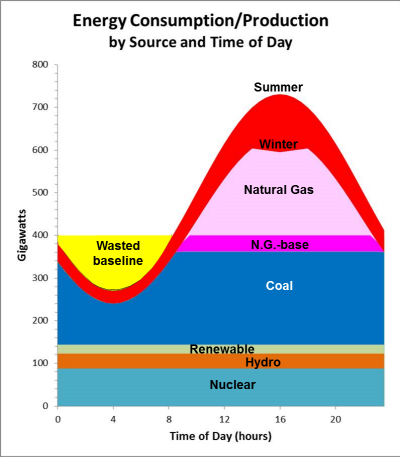
The section of the figure labeled "Wasted baseline" represents generating capacity that is not used because the demand is too low. The cumulative gigawatt hours of power represented by this section comprises the most obvious opportunity for better management of the energy supply. If this available energy is captured and stored, then it can be used during the peak hours, reducing the need for the total capacity during those hours, specifically the capacity generated by natural gas or coal. On the other hand, there is a strong case for additional nuclear power for national energy independence and greenhouse gas reduction; however, the requirement for constant temperature operation would increase the amount of wasted energy during hours of off-peak demand.  Having the very efficient Sisyphus energy storage solution completely remedies this problem.

Calculating the value of a storage solution in detail is very difficult, as costs of capital, variability from day to day and season to season, etc., enter into the math. Further, these details differ over the various parts of the country. However, the problem of calculating this value becomes easier if the storage solution involved many local solutions in the same way that the entire power system involves local generating plants and demand areas. With this caveat, there is a simple proxy: the hourly cost of power. Power systems throughout the country have different rates that are charged to major customers (and in some cases, to residential customers). In general, the rates during off-peak hours are much lower than during peak hours. The proxy yields a simple formula: sum the energy price times the "wasted baseline" (at the local level) to yield a purchase cost. Then, sum the energy price during peak hours times the recovered energy (purchased energy quantity times the storage system efficiency factor) to yield a sales price. Subtract the purchase price from the sales price. As shown in Equation 1, if the result of these calculations is larger than the storage system cost, then the storage system saves money (or yields a profit).

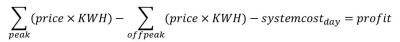   Equation 1.  Profit Equation

ENERGY STORAGE

Currently, we are not able to store energy in meaningful quantities.   Figure 2 shows the global stored energy capacity by storage type (described later). Pumped hydro accounts for more than 99% of this capacity. The total U.S. electrical generation is about 1100 GW and the U.S. pumped hydro capacity is about 40 GW. Thus the U.S. energy storage capacity is only about 3.6% of the total generation capacity.

Figure 3 helps explain this division. This figure (modified from an EPRI figure) shows the total capacities of each energy storage type (given the economic sizes of the systems) versus their discharge times. Certain uses require positioning in different areas of the figure. Uninterruptible Power Sources (UPS) require very quick discharge times and (generally) smaller power ratings. Support for load shifting within the power grid requires medium power ratings and variable discharge times. Bulk power management (the primary subject of this project) requires large power ratings and medium to large discharge times. System cost per MW is also a factor, but Figure 2 and Figure 3 do not address system cost.  This will be discussed in the Power Source Comparisons section.

Pumped hydro relies on the simple physics of potential energy: moving a mass away from the center of the earth requires energy, which is stored as potential energy (minus efficiency losses). Returning the mass to a lower level enables the recovery of this energy and conversion to electrical energy (minus efficiency losses). In pumped hydro systems, water is pumped at very high pressure into a much higher storage reservoir.  This requires a large and costly dam with huge pumps. When the energy is required, the water is allowed to flow down through a turbine generator to recover the energy. The efficiency of pumped hydro (recovered energy/input energy) is about 70%.

Compressed Air Energy Storage (CAES) also relies on simple physics: air is compressed into a chamber and then used to drive a generator to recover the energy. CAES has at least two major problems. The first is that compressing air also heats the compressed air. If this heat is lost prior to recovering the energy this results in an additional efficiency loss. The second problem is that for large scale uses, the air is compressed into a cavern, which is inherently dirty. The expanding air that drives the generator carries some of this dirt into the generating system.

Flywheels are simply very massive wheels. Energy is stored by spinning the flywheel to higher revolutions per minute and recovered by using the rotation to drive a generator (reducing the speed). Superconducting Magnetic Energy Storage (SMES) stores energy as a direct current flow in a superconducting coil. As shown in the figure, SMES systems are capable of medium power ratings and have extremely short discharge times. They also have very high efficiency values, generally greater than 95%. Batteries of various types are also used for energy storage. Only those that have potential for large scale use are shown in Figure 3. Cost is a major factor for batteries since the power rating scales linearly with the required number of batteries.  As the required number of batteries increases, the cost does also.

Sisyphus, the subject of this proposal, addresses all of the foregoing issues and provides superior solutions for the needs of national and worldwide efficient energy management. This is represented in Figure 3 showing how Sisyphus systems cover the ideal area for bulk power management. The sections below will also demonstrate that Sisyphus can achieve these benefits at very favorable costs.

Figure 2.  Energy Storage Types


Figure 3.  Storage Discharge versus Power

 

SISYPHUS OVERVIEW

The Sisyphus system for energy storage takes its name from the myth of Sisyphus, who was forced by the Greek gods to roll a massive boulder up a hill every day, only to have it roll back down during the night. He had to repeat this process forever. The Sisyphus energy storage system stores energy by transporting massive blocks uphill during off-peak hours (night rather than day) and recovers the energy by their return to the bottom during peak hours (day rather than night). The picture to the right (Figure 4) is Titian's painting of the myth, painted from 1548-1549.

The Sisyphus system uses the same basic physics as the pumped hydro systems, storing electrical energy as potential energy and then converting that potential energy back into electrical energy.  However, there are several important differences:

• The masses are moved by a solid state linear induction motor and the energy is recovered using the same solid state equipment as a linear induction generator, eliminating the need for massive pumps and generators and their efficiency losses and repair needs.
• The masses are moved by a solid state linear induction motor and the energy is recovered using the same solid state equipment as a linear induction generator, eliminating the need for massive pumps and generators and their efficiency losses and repair needs.
• The masses ride on vehicles supported by lossless superconducting magnets, eliminating most electrical and friction-type losses, leading to very high overall efficiency.
• The Sisyphus system is expected to have 90-95% efficiency, rather than the quoted ~70% efficiency of pumped hydro (which does not account for the lengthy times when pumped hydro has been off-line due to equipment repair and replacement of the huge pumped hydro turbines).
• The Sisyphus vehicles have no physical contact with the guideway, except though magnetic levitation, eliminating all frictional wear and tear of the components.
• The rate of energy recovery can be varied simply by varying the rate of vehicle movement, allowing for more or less rapid discharge rates when desirable.
• Sisyphus systems can be built economically in smaller units than is possible for pumped hydro, allowing for greater flexibility.
• Sisyphus systems can be built in about a third the time required for a pumped hydro system for lower costs per equivalent energy storage.
• Like pumped hydro systems, Sisyphus requires a height differential; however, it does not require topography suitable for building a reservoir. In fact, it can be built on the side of any mountain (Figure 5) or in an underground mine (Figure 6).

Further, like pumped hydro and unlike batteries, flywheels and SMES, the scaling cost of Sisyphus depends on an increase of the low cost elements (concrete blocks), not on the increase of the high cost elements.
 

Figure 4.  Mythological Sisyphus

Figure 5.  Siting Sisyphus on a Mountain
 

      Figure 6.  Siting Sisyphus in a Mine Shaft
 

SISYPHUS TECHNOLOGY

The Sisyphus system for energy storage embodies several technologies, some simple and some complex.

Operating Technologies

As shown in Figure 7 and Figure 8, the Sisyphus system is composed of several parts. There is a storage area at the low end of the system and a storage area at the upper end of the system. The concrete block masses are stored in these. There is a guideway connecting the two storage areas and vehicles that carry the blocks on the guideway, moving them from one storage area to the other. Not shown are the connections to the power grid, the power conditioning equipment and the electronic controls.

Figure 7 shows the system in motor mode. Power is drawn from the grid to move the vehicles carrying the blocks from the lower storage area to the upper storage area, converting almost all of the electrical energy into recoverable gravitational potential energy. Vehicles are loaded from the lower storage area. Loaded vehicles move up the hill and deposit the blocks in the upper storage area. Empty vehicles move down the hill to get more blocks. The system is operated in this mode during off-peak hours when the energy cost is low and proceeds until all of the blocks are moved up hill.

Figure 8 shows the system in generator mode. The blocks from the upper storage area are loaded onto vehicles, which then slide down the hill, converting almost all of the potential energy into electrical energy. Loaded vehicles deposit the blocks at the lower storage area and move up the hill to get more blocks. The system is operated in this mode during peak hours when the energy can be sold at the highest price and proceeds until all of the blocks are moved down the hill.

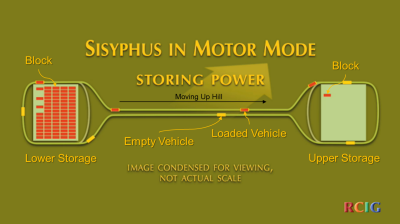
Figure 7.  Motor Mode


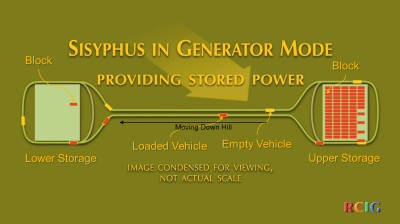
Figure 8.  Generator Mode
 

The vehicles have rollers on a tilt-able bed supporting the blocks so that the blocks can be rolled off into the storage areas. The storage areas have slanted beds of rollers, with brakes, so that the blocks roll toward the far side and can use gravity to roll the blocks onto the vehicles on the far side. Figure 9 is an illustration of one possible configuration of the storage yard subsystem, with blocks having just been loaded onto four vehicles.

The difference between the purchase price for the electricity and the sales price for the delivered electricity is the operating profit. The system has greater than 90% efficiency, meaning that the delivered power is more than 90% of the purchased power.

A short movie illustrating the Sisyphus operation, , click on the camera symbol.

Figure 9.  Storage Yard
 

Guideway Technologies

The guideway acts as the non-contact track for the magnetically levitated vehicles of the Sisyphus system.  Each side of the guideway has a set of panels attached that contain the aluminum coils that comprise the guideway half of the motor/generator system.  The guideway is composed of a series of prefabricated beams. Each guideway beam is made of polymer concrete, which avoids the need for rebar strengthening. (Rebar would react magnetically to the moving superconducting magnets on the levitating vehicles.)

Figure 10 shows a cross-section of the vehicle and the guideway. This view shows the relationship of the superconducting magnets on the vehicle and the aluminum loop panels mounted on the sides of the guideway beam. The guideway is shown resting on grade; however, in certain applications, it could be mounted on pillars in the same fashion as the Disneyland Monorail.

Figure 11 shows an actual section of guideway. In the picture, it is sitting on a semi-trailer (you can just make out three wheel sets at the left end, below the guideway beam.  This and subsequent photographs were taken during a $13 million test project performed in Florida.
 

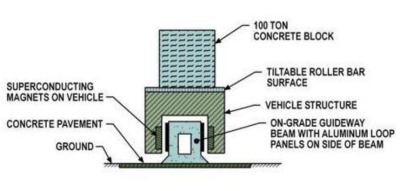
Figure 10.  Guideway Cross-section Schematic


Figure 11.  Guideway Beam
 

Motor/Generator Technologies

The levitation/motor/generator system consists of two components, the superconducting quadrupole component and the non-superconducting aluminum coils. The quadrupole component contains four coils of superconducting wire that support an enormous lossless current.  As long as the coils are maintained at the necessary low temperatures, these currents generate extremely strong magnetic fields. These fields interact with the aluminum coils, inducing currents and opposing magnetic fields. The magnetic fields play two roles: levitation and propulsion / power generation effects. 

The interactions of these fields create the magnetic levitation effect, keeping the vehicle several centimeters above the guideway. The levitation may be supplemented by adding iron plates to the top of the guideway beam.

Figure 12 is a CAD/CAM perspective view of the quadrupole component, showing the four containment boxes and the cooling connections running between the pairs. The superconducting coils are in the containment boxes that keep the loops in a superconducting state and the cooling apparatus that maintains the temperature of the containment boxes is the long box between them. Looking at the side, the two loops have currents circulating in opposite directions, so that the flow where the vertical parts are closest is in the same direction (up or down) for the two loops.

 
Figure 12.  Quadrupole Perspective View
 

• It shows four sets of paired coils colored blue. These are the vertical stabilizer coils. They act to raise the quadrupole unit if it drifts too low and to lower it if it drifts too high. This action is generated solely by the induced currents created by the quadrupole and does not require any external forces or actions (such as software controls). In addition to gross vehicle movement, these actions also automatically correct against tilting of the vehicle.
• Figure 13 also shows four coils colored green. These coils are paired with the coils on the other side of the guideway and act to shift the quadrupoles (one on each side of the guideway) to the left or right to retain horizontal centering.
• Finally, Figure 13 shows one coil colored red. This is the powered drive coil. Electronic switching connects it to power only when the quadrupole is present. Adjoining panels are identical in construction; however, the current circulates in the opposite direction. The power feed is a sinusoidal alternating current, so that the direction reverses during each cycle.
  • In the motor mode, power is fed to the coil inducing the impulse to push the quadrupole in the desired direction. This is accomplished through the alternating current direction and the opposed circulations in the quadrupole (Figure 14).
  • In the generator mode, power is drawn from the coil as the quadrupole moves past it. This slows the quadrupole, maintaining the desired speed, as the acceleration of gravity acts to increase the speed of the quadrupole. At the bottom of the hill, the quadrupole is stopped, drawing the last of the potential energy from the quadrupole, vehicle, and block.

Figure 14.  Propulsion Coils

Figure 15 is a photograph of a set of aluminum coils prior to being encased in polymer concrete to fabricate the panel.

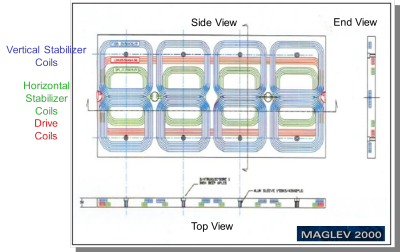
Figure 13.  Aluminum Coils Schematic


Figure 15.  Aluminum Coils Photograph

Intellectual Property and Magnetic Levitation Applications

James R. Powell and Gordon T. Danby created and patented a number of inventions in the field of superconducting magnetic levitation.  Powell and Danby presented their original concepts in 1966 and received a patent in 1968. The original concept used low temperature superconducting (LTS) magnets (cooled with liquid helium). In 2000, they were awarded the Benjamin Franklin Medal in Engineering by the Franklin Institute for their work. Powell and Danby later improved their concept by using quadrupole superconducting magnets, rather than dipole magnets. The original quadrupole magnets are also LTS magnets; however, newer designs use high temperature superconducting (HTS) magnets (cooled with liquid nitrogen). Relevant patents for Sisyphus are listed in Table 1 below.

Table 1.  Intellectual Property Patents

Starting in 1969 the Germans built a magnetic levitation transportation system using non-superconducting magnets. By 1993 they achieved 450 km/hour speeds. The separation between the vehicle and the guideway must be constantly monitored and corrected due to the unstable nature of electromagnetic attraction.  The system's inherent instability and the required constant corrections by outside systems may induce vibration. This system requires very costly guideways because the magnets are weak (~1 cm gaps) and has no ability for track switching. This system is in use in Shanghai, China.

Starting in 1972 the Japanese built a magnetic levitation transportation system using Powell and Danby's original concept. By 1997 they achieved 550 km/hour speeds. Strong magnetic fields (from the dipole superconducting magnets) on the train require the use of magnetic shielding to protect passengers with pacemakers and magnetic data storage media such as hard drives and credit cards.  The superconducting magnets do allow greater gaps between the magnets and the guideway; however, the guideways for this system are very costly. Track switching is possible, but difficult.

SISYPHUS IMPLEMENTATION

The implementation can be divided into four parts, the physical definition of the system, the costs of the system, the projected financial results, and the implementation phasing.

Physical Definition

Figure 16 shows a view of the proposed site for the demonstration Sisyphus system. The line between the yellow pins is the TVA right of way for power line down from the wind farm on top of Buffalo Mountain. The lower storage yard will be sited at the lower yellow pin. The upper storage yard will be sited in the flat area below the upper storage pin.

Figure 17 shows a schematic perspective view of the system, showing the relative sizes of the storage yards and the guideway linking them.

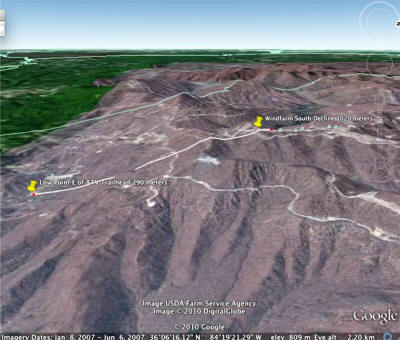
Figure 16.  Buffalo Mountain
 

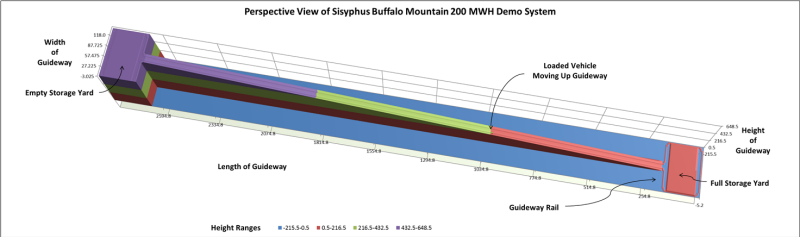
Figure 17.  Perspective Schematic of Buffalo Mountain System

The demonstration Sisyphus system has a nominal energy storage rating of 200 megawatt hours (MWH). That is 200 MWH are stored by the system. With an efficiency rating of >90%, this means that ~180 MWH will be recovered. The storage rating is defined by physical parameters of system height (640 m), weight per block (100 metric tons), and number of blocks moved (1148). The potential energy stored in one 100 metric ton block raised 640 m is 0.1742 MWH.  Lifting 1148 blocks stores 200 MWH.

Keeping 1148 blocks alternately at the foot of the grade and the top of the grade requires two storage yards of ~3.2 acres, each. The layout also requires ~6300 m of guideway. Vehicles will move at ~60 miles per hour between the storage yards. Higher speeds are easily possible; however, efficiency losses from increased wind drag reduce the value of higher speeds. It will take the vehicles 14 seconds to reach 60 mph and 14 seconds to decelerate. With an estimated 50 seconds to load a block and 50 seconds to unload it, the total round trip time is about 4 minutes. In order to lift all 1148 blocks during the off-peak hours, 12 vehicles are required ((4 min x 1148 blocks / 12 vehicles) / 60 min/hour = 6.4 hours). Because the peak time is longer than 6.4 hours, the rate of energy recovery can be varied from rapid to slow, depending on needs.  In addition to the vehicles, guideway, and blocks, the storage areas will need handling equipment and the entire system requires electrical control and power conditioning subsystems. This Sisyphus system requires no investment in land, as the TVA right of way is sufficient to contain the system.

System Costs

The system costs are divided into investment costs to build the system and annual costs for its operation, as shown in Table 2. The total investment cost of $60 million is based on current best estimates of costs of the various components of the system. This figure also shows up as a 30 year straight-line amortization in the annual costs. The cost of purchased energy is based on an estimate of 8 cents per KWH ($80/MWH) for energy purchased off-peak.

Table 2.  Demonstration System Costs

These cost estimates are based on the assumption of multi-unit production. The first Sisyphus system will incur additional setup costs, which are described in the implementation phasing section below.
 

Projected Financial Results

The financial results are divided into gross revenue (delivered energy times price), net revenue (gross revenue minus energy purchase costs and operations & maintenance costs), and profit (net revenue minus amortization costs), as shown in Table 3. The price of energy sold is based on an estimate of 20 cents per KWH ($200/MWH) for energy sold at peak prices. The quantity of energy delivered is 90% of the quantity purchased. The Return on Investment (ROI) is the Net Revenue as a percent of Total Investment.

Table 3.  Projected Demonstration System Financial Results

1000 MWH Upgraded System Financials

The financial results for the upgraded system are shown in the same formats as for the demonstration system (Table 4 and Table 5). Note that the Investment figures are totals for building this system and include the costs for the demonstration system. The increase in profitability is due to the efficiency of scale, as the energy costs and sales come to dominate the other costs.

Table 4.  1000 MWH System Costs

Table 5.  Projected 1000 MWH System Financial Results

Implementation Phasing

The creation of the first Sisyphus system, the demonstration system on Buffalo Mountain, TN, requires additional setup costs. These setup costs involve creating engineering drawings and tooling and extensive testing to establish the workability of the concepts and refine the costs. Workability will be defined by the Technology Readiness Level (TRL) metrics.

The work will proceed in six phases, as shown in Table 6. Each phase has short definition and a goal describing what will be achieved during the phase. For each phase of the demonstration system, the estimated labor and material costs are shown, along with the total cost for the phase and the phase duration. The totals for all phases of the demonstration system are also shown. The estimated total cost and time to upgrade the system to the 1000 MWH Sisyphus system are shown as Phase 5.

Table 6.  Sisyphus Phases

Rapid Load Balancing

In the physical description of Sisyphus above, the top speed of the vehicles was set at 60 mph and the trip time to load a block, travel to the other storage yard, and unload a block was calculated as 4 minutes.  This resulted in a minimum time to move all the blocks from one storage yard to the other of 6.4 hours (for the 200 MWH demonstration system).  Given 90% efficiency, 180 MWH would be recovered in 6.4 hours, yielding an average power rating of ~28  megawatts.  However, some local situations might require more power for load balancing.  Increasing the vehicle speeds would yield lower trip times and produce more power; however, the power peaks at 90 mph and decreases after that due to the ratio of acceleration time and time traveling at maximum speed.  These calculations assume constant efficiency, but efficiency will decrease with increasing speed due to wind resistance.  Even without wind resistance increase, the amount of power increase from 60 to 90 mph is only about 4%.

Increasing vehicle frequencies will also yield more power.  The 6.4 hour time assumes that subsequent vehicles start loading about 20 seconds after the previous vehicle starts loading.  The 12 vehicles could be set to start loading about 10 seconds after the previous vehicle started, giving a 60% increase in power during the time for the 12 vehicles to descend; however, the vehicles would have to return to the top, with no power being recovered during the interim.  Figure 27 graphs the power (green curve) generated by 12 vehicles for different separation times (measured on the left axis).  It also shows the lag time (bent straight line) before the first vehicle (calculated as the 13^th vehicle) can start generating power again.  As the separation time is reduced to about 20 seconds, this curve (measured on the right axis) drops because the only gaps between vehicles are the separation times.  However, separation times less than 20 seconds require that the available 12 vehicles bunch up, leaving larger and larger gaps between the bunch of 12 vehicles.

The implication of these calculations is that Sisyphus can generate bursts of power over short time frames.  However, such a burst of power must be paid for with a delay until more power can be produced.  As shown in Figure 27, with all 12 vehicles running in a single bunch (zero seconds separation), the maximum power is generated at a cost of maximum recovery time (240 seconds = 4 minutes)

Figure 27.  Power and Time to the 13th Vehicle Depend on Vehicle Separation