(from a talk given at Oak Ridge National Laboratory in 1986)
| Project Metadata | Keywords | ||||||||||||||||||||||||||||||||||||||||||||||||
|
|
I. INTRODUCTION
One of the hardest tasks involved in modeling is ensuring that the model is used in a way consistent with its assumptions. Users often do not like to examine the assumptions of a model. They want to use it. In their view, the designer's job was to ensure that the model would be relevant for every conceivable use, in all circumstances, with no caveats. While this may seem unreasonable, it is not far from the true feelings of users. Since it is the user who is buying the product, it behooves the modeling community to be aware of the situation and act to ameliorate the situation.
Let me take a few minutes and describe a rather important example of a failure. Several years ago, the Air Force built a model called TAC CONTENDER. This was a model of the air war in a conventional war. It was to be used to determine optimum force mixes and strategies both for such things as Mutual Balanced Force Reduction and purchasing aircraft. It was scientific: it used Game Theory and concepts taken from Dynamic Programming. It was easy to use. It was wrong! (That is, the answer it gave was not the answer it was assumed that it gave [1].)
There are five technical issues involved in the failure of the TAC CONTENDER model: Game Theory, Pure and Mixed Strategies, Dynamic Programming, Bandwidth, and Adaptive versus Non-Adaptive Strategies. In addition there is the problem of presenting the user with a reasonably simple way to understand the impact of the technical issues on the valid use of the model and the interpretation of the results. I will discuss each of these points and their relationships.
II. GAME THEORY
Game Theory is that branch of mathematics from which the concept of minimax derives. Consider some arbitrary zero-sum (what one gains, the other must lose) confrontation, conflict, or game between two players. Suppose that each player has several alternative plays (or strategies) at his disposal and that for each pair of plays (one by each player) there is some well-defined outcome. We will consider only one play by each player for now. Generally, if you examine all the possible pairs of plays, some will be better for one player and others better for the other player. Given certain constraints on the game, there will be a best outcome for each player, with one or more pairs of plays yielding this outcome. If the outcome is realizable as a single real number, we may assume that the most desirable outcome for the Red player is the minimum of the set of all outcomes and the most desirable for the Blue player is the maximum. If the game involves simultaneous plays by the two players (or sequential plays with no information for the second as to how the first played), then we see that, in general, neither Blue nor Red can ensure that a play which can yield his desired outcome does yield it. However, Game Theory says that in certain suitable games, there is a "mutually enforceable" solution. That is, Red can ensure that the outcome is no larger than X, while Blue can ensure that the outcome is no smaller than X.
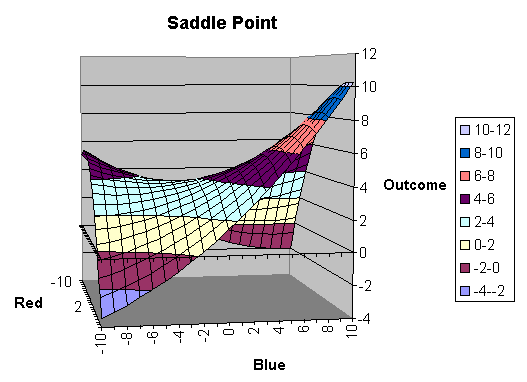
The "saddle point" diagram illustrates this notion. You can see that either a choice of -10 or 10 can lead to very low valued outcomes (favorable to Red); however, if Blue plays -10 when Red plays -10 or Blue plays 10 when Red plays 10, the outcome is very large, favoring Blue. Game theory states that Red's best overall strategy is to evaluate each play (from -10 to 10) and find the one with the minimum maximum value (minimax). This minimax ensures that no matter what choice Blue makes, Red can do no worse than the minimax. Blue's best strategy is to evaluate each play and find the one with the maximum minimum value (maximin). This maximin ensures that no matter what choice Red makes, Blue can do no worse than the maximin.

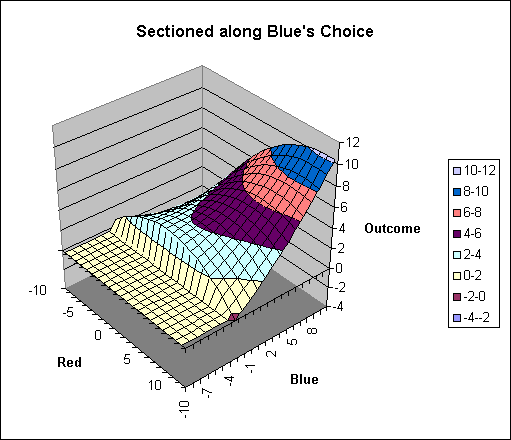
The diagram sectioned through Blue's choice shows how Blue may limit the damage that Red can do, while allowing for better outcomes if Red does not use the best strategy.
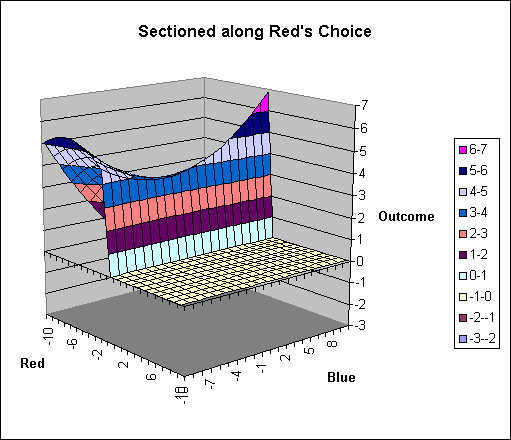
Similarly, the diagram sectioned through Red's choice shows Red's opportunity. Notice that in this particular game the amount of variability favors Blue, although the game is set to have a neutral minimax (and maximin) of 3.75.
Please notice that I have drawn the game in such a manner that it is clear that there is a minimax and so that it is clear how disastrous it can be to play for the best possible outcome and take a chance on the other side playing poorly. There are real problems of deciding whether a given "game" has a global minimax or multiple local minimaxes or a minimax at all! Additionally, there is a question as to whether people are so rational as to play the game this way.
This last question is the one which the users of TAC CONTENDER actually addressed well. In matters of force mix evaluation, the final measure of merit is performance; yet historically, performance has always been strongly affected by "extraneous" factors: tactics, strategy, training, motivation, maintenance, chance, etc. To choose a particular set of values for these variables leads to controversy outside the area of concern. Hence it was desired to measure the force mix options as to their performance with optimal tactics used by both sides. In this way, if some particular force mix were seen to be better than another in the model, the comparison would be subject to less debate.
III. PURE AND MIXED STRATEGIES
Having settled that using a Game Theoretic model has some advantages as a useful tool, practical problems arise as to implementing this mathematics in a model. I have shown you a nice, differentiable game; however, the air war in Europe is not known to have such a mathematical expression. It is here that the matter of Pure and Mixed Strategies arises.
In the model, the possible air activities are divided into four groups, Combat Air Support (dropping bombs on the battlefield), Battlefield Defense (shooting at the opponent's airplanes over the battlefield), Airfield Attack (bombing the opponent's airfields and airplanes on the ground), and Airfield Defense (shooting at the opponent's airplanes over your own airfields). The winner is assumed to be the one who drops the most tons of bombs on the battlefield. In order to make the game a zero-sum game, the measure used is Blue tons minus Red tons (net tons). A pure strategy is an allocation of available airplanes to these activities ([100%,0,0,0], [25%,25%,25%,25%], etc.) On any given day, the starting point of available airplanes, the selected pair of pure strategies, and the effectiveness parameters together determine the drawdown of aircraft and the tons of bombs dropped. (The drawdown of aircraft and the input resupply will determine the next day's starting point.) Thus for a given day of the battle, the pair of strategies will determine one point of the game function. Naturally, the more realistic the drawdown function, the slower the computation of this one point.
In the model, the possible number of Pure Strategies considered is limited to a small finite number. Thus the model can only directly examine a subset of the possible plays. Further, there is no guarantee that a saddle point exists. At a saddle point the minimax equals the maximin and this is the Game Value. If there is no saddle point, the Game Value lies between the minimax and the maximin. The difference between the minimax and the maximin is a region of non-enforceability. That is, there is no guarantee as to how close the actual result will be to the top or the bottom of the range. The Game Value is the expected value which will be achieved. There is a technique for calculating the Game Value, whether there is a saddle point or not. This is the Brown-Robinson Algorithm.
Roughly described, from a starting point, outcomes are determined for choices from a predetermined set of pure Blue strategies while holding Red's choice constant. If no worse outcome for Blue is found, and a similar search along Red's choices discovers no worse outcome for Red, then the starting point would be a minimax for this subset of the total possible Pure Strategies. In general, the starting point does not the satisfy the conditions of a minimax and a search is instituted. The feature which makes the eventual outcome an approximation of the Game Value for the entire set is a set of weighting factors which are built as the search proceeds. These weighting factors look like coefficients for the Pure Strategies, e.g., 10% of [100,0,0,0], 90% of [25,25,25,25], 0% of the rest. When the search converges sufficiently, the set of Pure Strategies and factors is called a Mixed Strategy. In a game meeting all the proper conditions, the outcome associated with this pair of Mixed Strategies will be within the convergence factor of the absolute minimax and maximin.
There is a problem of interpretation which arises at this point. I stated earlier that the use of TAC CONTENDER was in the area of Force Mix decisions. However, at the end of the game, the model prints not only the outcome, but also the mixed strategies of each side. How can one avoid wanting to interpret this as telling how the war should be fought! This is what was done. Unfortunately, it is not clear that this is valid. The theory of the algorithm claims that these factors are interpretable as probabilities, that if the war were fought 100 times with the first Pure strategy being used 90 times and the second 10 times, then the average of the outcomes will be as stated. The implication is that the proper strategy for actually achieving the Game Value is not stated and may not be related to these two Pure Strategies at all! Certainly there is no stated justification of assuming that the correct strategy is
[.10 x 100 + .90 x 25, 0 + .90 x 25, 0 + .90 x 25, 0 + .90 x 25] = [32.5,22.5,22.5,22.5].
IV. DYNAMIC PROGRAMMING
A further complication which reality imposes on the war model is the multi-decision game. In a war one might expect up to three aircraft sorties per day for each day of the war. Each one of these sorties may be regarded as a one stage game as described above. The problem lies in connecting these separate games. The straight- forward method of letting the results of the previous game be the starting point for the next game in a single pass through the war has the advantage of simplicity. Unfortunately, it can lay no claim to optimality, as there exist examples of games for which such a process is demonstrably non-optimal.
One possible solution would be to consider the entire war as one large game with one play consisting of a choice of strategies for each substage of the larger game. This method was not chosen due to the enormous computational difficulties. Another possible solution was suggested by Dynamic Programming, a technique for working backward from a desired solution through each stage to the beginning, obtaining an optimal overall solution.
While the algorithm used in TAC CONTENDER is not a Dynamic Programming algorithm, it does take many characteristics from this method. One of the model's authors described the logic as "forward" Dynamic Programming. The concept involves adding an additional measure of merit to that of bombs dropped on the battlefield, and optimizing on the resulting measure. The additional factor is surviving airplanes. The combined measure of merit is the net potential of surviving aircraft for dropping bombs on the battlefield.
The algorithm needs a starting estimate of the aircraft potential for each day of the war. That is, on the last day of the war, how many tons can the aircraft drop, on the next to last day what is the potential considering the aircraft might drop bombs or prevent opposing aircraft from dropping bombs, etc. Each stage is played with the object being the optimization of this potential and the results passed to the next stage. Data is obtained about the performance of the war which is used to modify the potentials. These modified potentials are used in the next iteration. The entire war is replayed through sufficient iterations for convergence (or exhaustion of a preset number of iterations).
The question of optimality arises about this algorithm. The authors of the model could not show any mathematical sufficiency for optimality; however, they hoped that the similarities to Dynamic Programming and the inclusion of the Game Theoretic stages would be sufficient to come close to the optimum result. This conjecture, together with the minimax-maximin difference discussed above generate the Bandwidth problem.
V. BANDWIDTH
Properly speaking, the Bandwidth problem is really two problems. One is the possible non-existence of a saddle point, and the resulting band of unenforceable outcomes. If this is the case, knowing the Game Value does not give any information on the size of this unenforceable band. The second problem is whether the stated Game Value of TAC CONTENDER is the actual Game Value, and if not, how far from correct is it. The claim made by the developers of the model was that the combined Bandwidth was acceptably small.
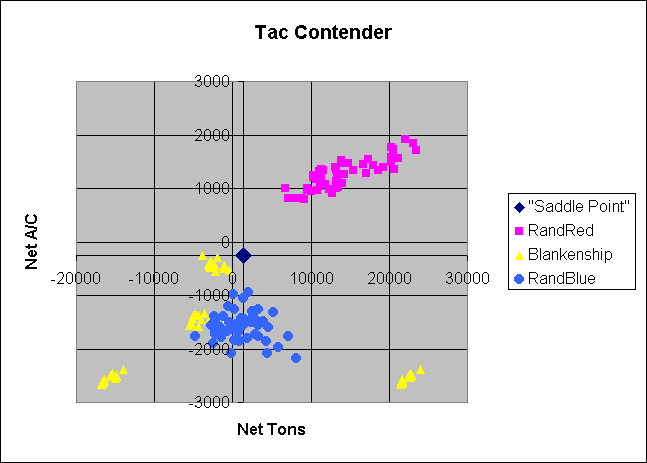
The study that Lt Col Cockrell and I did was not a mathematical analysis; it was a brute force kind of thing. We simply made the model play random strategies against the supposed optimal ones. If there were a saddle point and TAC CONTENDER found the Game Value, then the outcome at that saddle point would equal the Game Value. In the game played the net tons are Blue tons minus Red tons, so all non-optimal Red plays (labeled RandRed) should yield higher than optimal outcomes, while all non-optimal Blue plays (labeled RandBlue) should yield lower than optimal outcomes. We also played a designed set of Blue options developed by Dr. Blankenship (labeled Blankenship). In the case where there is no saddle point, random Red and Blue plays might pass the Game Value, but would not pass the maximin and minimax values, respectively. Since TAC CONTENDER does not generate these values, the only test for this is the extent of any crossover as to useability.
The outcome graph shows that either TAC CONTENDER fails to find the Game Value or the game has no saddle point since several Blue values for net tons are larger than the TAC CONTENDER result (labeled "Saddle Point"). The fact that almost half the random Blue sample surpass that result and the size of the difference indicate that the result is not very useful as an optimal Game Value. The graph also shows the net aircraft remaining as if it were the measure of merit. The results indicate that the model could be generating a minimax for that measure.
VI. ADAPTIVE VERSUS NON-ADAPTIVE STRATEGIES
The final technical issue has to do with the interpretation of the daily strategies used in TAC CONTENDER. The foregoing discussion assumed a Non-Adaptive interpretation. This is a mathematically stronger interpretation. That is, if a set of strategies for the whole war can be found whose outcome is a saddle point for the supergame consisting of the entire set of daily games, then there is no better set to be found.
An Adaptive Strategy is a function which defines the play for each daily game, depending on the start point for that day. Thus, an adaptive strategy is a rule which evaluates to a set of choices, whereas a Non-Adaptive Strategy is a set of choices. For a game with no Non-Adaptive Strategy saddle point, there is still some hope, as it may have an Adaptive Strategy saddle point.
The general consensus had been that TAC CONTENDER yielded the optimum Game Value using Non-Adaptive strategies; however, one of its authors claimed that this was a poor interpretation, that it should be viewed in the Adaptive strategy sense. While this made some intuitive sense in that the process of deriving the output strategies and outcome was certainly adaptive, in the English language definition of "adaptive," there was no visible function which could be called the Adaptive Strategy, nor any support other than a bare contention that this was the case.
Having shown that TAC CONTENDER was, at best, a poor approximator to the Game Value when its output strategies were used in a Non-Adaptive interpretation, Cockrell and I investigated the Adaptive case. First, we determined that the model itself was a set of Adaptive strategies. That is, it develops a function of a particular form which defines the play for each daily game, depending on the start point for that day. The whole war iteration process defines aircraft potentials which, together with the daily Brown-Robinson Algorithm, define the daily play. The question then became whether or not the set of Adaptive Strategies which TAC CONTENDER can generate is a good set.
Lacking the ability to solve, or even properly state, the mathematical question, we resorted to tests. We fed the model the same sets of forced strategies as reported above; however, rather than requiring the model to play the "optimal" (original output) paired strategy, we allowed it to adapt to the input strategy. In every case the model found a clearly superior strategy to play against the forced input. While this could not prove anything regarding the optimality of the TAC CONTENDER Adaptive Strategy, it did lend some credence to that possibility.
VII. CONCLUSIONS
As you may imagine, this investigation caused consternation in some circles: studies were re-examined to determine the impact, proponent organizations argued against publishing the results, organizations with competing models were gleeful, etc. Still, this was one of the finest models of warfare I have ever seen: it was sophisticated and slick in execution, used leading edge mathematical and programming techniques, and was relatively user-friendly. What should have been done?
Hindsight is a wonderful thing. At this point, I would suggest detailed comparison of results on several well designed games with known saddle points between the TAC CONTENDER methodology and one or more of the now extant (computer hog) programs which are mathematically valid. This would start to define the parameters of reliability of TAC CONTENDER's results as an Adaptive game. On a more realistic set of games, I would suggest an interactive set of runs with human strategists. This would define the parameters of believability in the model as a good strategist. If it passed these tests, it might again be acceptable in its original role (with printed strategies suppressed).
In the normal course of model development the model is usually finished just after it must be used. This puts a definite crimp on any validation process such as I suggested above. In such an event, claims for the model had best be as conservative as possible. However, the assumptions and domain of applicability of the model must be stated as clearly as possible in the Executive Summary of the model. Any undetermined areas must also be included. This will prevent the misuse and/or later embarrassment of the model builders.
Naturally, there is the concern that such caveats will be viewed as failures of the model and lead to disuse and dissatisfaction with the model and its builders. My experience with the users in the Joint Chiefs of Staff was precisely the opposite. Most of them were not sophisticated modelers, although some were, and most were not sophisticated in mathematics and operations research, although some were. But all of them were interested in doing the best job possible in analyzing the problems at hand. They were not at all afraid to use heuristic techniques or use their military expertise to fill in gaps, but they wanted to make sure they knew when this was done so they could deliver their considered opinions on the reliability parameters of their results.
REFERENCE
Hartley, Dean S., III and Allen A. Cockrell. An Examination of a Distribution of TAC CONTENDER Solutions. Code B-235, National Military Command Systems Support Center, DCA, Washington, DC, 1974.
If you arrived here using a keyword shortcut, you may use your browser's "back" key to return to the keyword distribution page.
Return to Hartley's Projects Page