
Page Last Updated: Tuesday, 19 January 2016 11:02 EDT, (c) 1973, 2007, 2008, 2016
Note: If SUV-infinity appears as SUV4, you may not have the font "WP MathA" installed. You may download the WP MathA and WP MathA Extended fonts with control+click on the following links: WPHV06NA.TTF and WPHV07NA.TTF. (Or you may find them at http://instruct1.cit.cornell.edu/courses/fontfix.htm.) Save the files to your Fonts folder (probably C:\Windows\Fonts). If you cannot save them there, save them somewhere else. Then right click on the file and choose "install." You may have to reboot for these to be applied by Windows.
| Project Metadata | Keywords | |||||||||||||||||||||||||||||||||||||
|
|
Abstract. In this paper, the concept of cellularity is extended to spaces which are not compact. The extension is called quasi-cellularity, where a quasi-cell is a regular neighborhood of a tree. This general extension splits into two concepts, strong quasi-cellularity and weak quasi-cellularity. Strong quasi-cellularity implies weak quasi-cellularity, but the reverse is not true. In the course of extending cellularity, an extension of the UV4 property is defined, called strong UV4, or SUV4, and it is shown that SUV4 is a topological property. It is demonstrated that a strongly quasi-cellular set embedded in an n-manifold, n$4, has the SUV4 property and satisfies a strong quasi-cellularity criterion. In like manner, a weakly quasi-cellular set embedded in an n-manifold, n$4, satisfies part of a weak quasi-cellularity criterion.
This research is a condensation of the first half of the author's Ph.D. dissertation, written at the University of Georgia under the direction of Professor R. B. Sher. I would like to express my thanks to Professor Sher for his aid. His advice and criticism have been invaluable.
AMS 1970 Subject Classifications. Primary 57A60, 57C99;
Secondary 57C40.
MSC 2000 Subject Classifications. Primary 57N60, 57Q99; Secondary 57Q40,
57Q65.
Key words and phrases. Cellular, cellularity criterion, properly Sk-inessential, quasi-cell, quasi-cellular, quasi-cellularity criterion, quasi-trivial, strong quasi-cellularity criterion, strongly quasi-cellular, SUV4, tree, UV4, weak quasi-cellularity criterion, weakly quasi-cellular.
NOTATION
UE and Int(U) symbolize the topological interior of
U.
MEi+1 symbolizes the topological
interior of Mi+1 (the apparent sequence of the
superscript and subscripts is purely an artifact of the HTML).
( €i)i=14
symbolizes an operation or group of indexed entities ranging from the index of 1
to the index of 4 (the apparent sequence
of the superscript and subscripts is purely an artifact of the HTML).
J+ symbolizes the set of positive integers.
ú1 symbolizes the real number
line.
Sn symbolizes the Euclidean n-sphere.
Mn and Xx symbolize n-dimensional
and x-dimensional objects, respectively.
Fi and Gi, where F and G
are maps, symbolize indexed maps, not n-dimensional objects.
F0 and F1, where F is a
homotopy, F:XHIàY,
symbolize F(X,0) and F(X,1), respectively.
MB symbolizes the boundary of
B.
-->> symbolizes an onto map.
Cl(X) symbolizes the topological closure of X.
K symbolizes
the complex closure of K.
FY symbolizes the Freudenthal
compactification of a space Y.
EY symbolizes the set of ends of Y.
` symbolizes a collapse.
1 INTRODUCTION.
The concept of cellularity is a well-known and useful concept. McMillan has shown [14, Theorem 1] that a UV4 compactum lying in the interior of a PL n-manifold, n$5, which satisfies his cellularity criterion is piecewise linearly cellular. It is also true that a cellular set is a UV4 compactum and satisfies the cellularity criterion if it lies in the interior of an n-manifold, n$3.
In this work, we extend the concept of cellularity to objects which are not compact. We define a quasi-cell to be a regular neighborhood of a tree, and use this as an analog of a cell. Because of certain differences between compact and non-compact objects, the extension splits into two concepts, strong quasi-cellularity and weak quasi-cellularity. We show that the concept of weak quasi-cellularity is properly contained in the concept of strong quasi-cellularity.
In the course of extending cellularity, we also define an extension of the UV4 property, called strong UV4, or SUV4, and show that SUV4 is a topological property.
We shall attempt to maintain standard notations and usage whenever possible. Dugundji [7] and Hudson [10] will be our references for general background material. We shall thus assume familiarity with the concepts of simplexes, complexes, polyhedrons, joins, triangulations, subdivisions, PL, combinatorial and topological manifolds, and simplicial and PL maps and homeomorphisms. We distinguish between topological closure and complex closure by Cl(K) and K, respectively.
Most of the spaces with which we will be concerned will be locally compact metric spaces. DIST(x,y) will refer to the distance from x to y using some (perhaps not explicitly named) metric. Some concepts obviously require a metric, even if none has been specified. For instance, the ε-neighborhood of a set X, N(X; ε), for ε>0, is the set of points having distance from X less than or equal to ε. Likewise, we need a metric for the concept of ε-homotopy: If H:XHIàY, where I=[0, 1], is a homotopy with ε>0 given, and for each p X, H({p}HI) has diameter less than ε, then H is an ε-homotopy.
The work below comes from the first half of [8]; however, there is additional background material in the Appendix of [8] that is not included. This material includes proofs on infinite regular neighborhoods, proper maps, mapping cylinders, general position, and engulfing theorems.
2 SUV4.
2.1 DEFINITION. A map f:XàY of topological spaces is proper if f -l(C) is compact whenever C is compact.
2.2 DEFINITION. A tree is a connected, simply connected, locally-finite l-complex.
2.3 DEFINITION. Suppose N is an n-manifold. If there is a PL n-manifold N'dEn which is a closed regular neighborhood of some tree, and if there is a homeomorphism h from N' onto N, then N is called an n-quasi-cell. If the dimension is obvious, or not relevant, N will be referred to simply as a quasi-cell.
2.4 DEFINITION. Suppose M is a topological space and X is a subset of M. If, for each closed neighborhood U of X, there is a closed neighborhood V of X contained in UE, a tree T, a map f:VàT, a proper map g:TàU, and a proper homotopy H:VHIàU such that H0 is the inclusion and Hl =gBf, the we say that X has the strong UV4 property in M; this being the case, we say that X has property SUV4 in M.
2.5 REMARK. Since H1 is proper, f must be proper also. In [18], Sher uses a slightly modified version of SUV4. He requires that f be onto T, which, along with gBf being proper, implies that g is proper. If X is connected, these two definitions coincide. In any case, if X satisfies the definition of [18], it satisfies Definition 2.4. If X is connected and satisfies Definition 2.4, then there is a single component V' of V containing X. Then f(V') is connected and is a tree. Let H':V'HIàU be defined by H'=H|V'. If g'=g|f(V'), then H'1=g'Bf|V' and f|V':V'-->>f(V') is onto. Since V' is closed, then H' is proper and X satisfies the definition of [18].
2.6 DEFINITION. Suppose M is a topological space and X is a compact subset of M. If, for each open neighborhood U of X, there is an open neighborhood V of X contained in U such that V is homotopic in U to a point, then we say that X has the UV4 property in M.
2.7 REMARKS. (a) It follows easily from the above definitions that a
space having UV4 or SUV4 must necessarily be connected.
(b) If M is a normal space and X is a compact subset of M
with the SUV4 property in M, then X has the UV4 property in M.
Obviously, properties UV4 and SUV4 depend on the ambient space M as well as the set X. For example, it can be shown that the "topologists' sin 1/x - curve" has property UV4, and hence SUV4, in any manifold M, but not in itself. However, McMillan has shown [15, Theorem 2, p. 20] that UV4 is a property which is topologically invariant with respect to embeddings in metrizable ANRs. The following theorem is the analog for SUV4.
2.8 THEOREM. The property SUV4 is topologically invariant with respect to embeddings in locally compact metric ANRs.
Proof. Suppose M and M* are locally compact ANRs and XdM, X*dM* are closed sets such that X has SUV4 in M and there is a homeomorphism onto, h:X-->>X*, and suppose U* is a given closed neighborhood of X*.
Since M is an ANR and UE* is open, UE* is an ANR and we may extend h to H on a neighborhood U of X into U*, H:UàU*, H|X=h. We may also choose U so that H is proper by means of [2, Lemma 3.2].

Figure 1. H:UàU*
Now, since X has property SUV4 in M, there exists a closed neighborhood V of X lying in UE, a tree T, a map f:VàT, a proper map g:TàU, and a proper homotopy K:VHIàU such that K0 is the inclusion and K1=gBf.
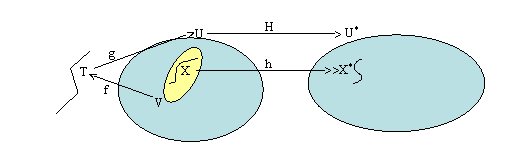
Figure 2. f:VàT and g:TàU
Let U1* be a neighborhood of X* lying in UE* and H*:U1*àU be a proper map with H*|X*=h-1. Let U2*=H*-1(VE), which is an open neighborhood of X* in U1*. Let ε:U*à(0,4) be any map. Since UE* is an ANR and HBH*|U2*:U2*àU* is a well-defined map which agrees with hBh-1=1U*|X* on X*, by [9, Theorem 1.1, Chapter IV] there exists a closed neighborhood V* and an ε-homotopy L:V*HIàU* with L0 the inclusion and L1=HBH*|V*. By AII.5 of [8], ε may be chosen so that L is proper.
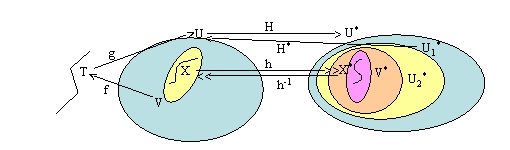
Figure 3. H*:U1*àU
Now define T*=T, f*=fBH*|V*,
g*=HBg, and K*:V*HIàU*
by
:L2t,
0#t#1/2
K*t= ;
<HBK2t-1BH*|V*, 1/2#t#1.
We have that V* is a closed neighborhood of X* lying in UE*, T* is a tree, f* is a map from V* to U*, g* is a map from T* to U*, and since g and H are proper, g* is proper. We have that K* is a homotopy (since L1=HBH*|V*=HBK0BH*|V*) and that K is proper since L, H, K, H* all are proper. We also have that K*0=L0 is the inclusion on V and K*1=HBK1BH*|V*=HBgBfBH*|V*=g*Bf*. Therefore X* has SUV4 in M*. €
Since all the ambient spaces with which we shall concern ourselves will be locally compact metric ANRs (usually manifolds), we shall speak of a set X having SUV4, rather than the embedding of X into a space having the SUV4 property.
2.9 REMARK. It can easily be shown that if A is an AR embedded as a closed subset of a locally compact metric ANR, T is a tree, and F:AHIàA is a proper homotopy with F0 the inclusion and F1(A)dT, then A has SUV4.
The following theorem gives an equivalent definition for a closed subset of an n-manifold, n$3, having SUV4.
2.10 THEOREM. Suppose M is a PL n-manifold, n$3, and X is a closed subset of M lying in ME. Then X has SUV4 in M if and only if for each closed neighborhood U of X, there is a PL submanifold V, with a non-empty boundary, such that XdVEdVdUE, a tree T embedded as a closed PL subset of M in UE, and a proper PL homotopy H:VHIàU with H0 the inclusion, H1(V)=T and H(VHI)dUE.
Proof. Suppose X has SUV4. Let U' be a closed neighborhood of X contained in UE. There exists a closed neighborhood V' of X in U', a tree T', a map f:V'àT', a proper map g:T'àU', and a proper homotopy H':V'HIàU' with H'0 the inclusion and H'1=gBf. Since X is connected, let VdVE' be a connected PL submanifold of M, with non-empty boundary, whose interior contains X. Since T' is locally compact, M is hausdorff, and f is proper, it follows that f is closed. Then T"=f(V)dT' is a closed tree.
Since n$3, g|T" is proper, and DIM T"=1, then there is a proper
homotopy L:T"HIàU'
with L0=g|T" and L1 a PL embedding. Define H:VHIàU'
by
:H'2t,
0#t#1/2
Ht= ;
<L2t-1Bf|V, 1/2#t#1.
We have that H:VHIàU'dUE is a homotopy (since H'1|V=[g|f(V)]Bf|V=L0Bf|V)
and is proper since H't|V, f|V and L are all proper. By construction,
H0 is the inclusion,
H1(V)=L1(f(V))=L1(T")=T,
and H(VHI)dU'dUE. Using general position, we can homotop H
to a PL homotopy in general position, staying fixed on the 0 and 1 levels, so
that we have the first half of the theorem.
The second half of the theorem follows trivially. €
3 QUASI-TRIVIALITY.
3.1 DEFINITION. A set X contained in the interior of an n-manifold is said to be quasi-trivial in M if X is contained in a quasi-cell in ME.
3.2 DEFINITION. Let K and L be topological spaces and f:KàL
a continuous function. Let (KHI)+L
be the free union of (KHI) and L, with
topology such that a set is open in (KHI)+L
if and only if its intersections with both KHI
and L are open in KHI and L, respectively.
Let R be the equivalence relation on (KHI)+L
generated by (x,1) ~ f(x) for all x in K.
Let P be the projection
P:(KHI)+Là[(KHI)+L]/R.
We shall say f is the attaching map of KHI
to L; [(KHI)+L]/R is written Mf,
and is called the topological mapping cylinder of f. We shall regard K as
a subset of Mf by identifying K with KH{0}
and noting that (KH{0})/R is still KH{0}.
We shall regard L as a subset of Mf since L/R is still L.
It can be shown that if K and L are locally finite simplicial complexes and f:KàL is a proper simplicial map, then Mf can be triangulated as a locally finite simplicial complex Cf with a subdivision K' of K and L and subcomplexes and Cf`L. See [5] for a discussion of the compact case and [8] for a generalization to the non-compact case. We take our theory of non-compact regular neighborhoods and collapses from [17].
The following theorem is quite similar to Lemmas 39 and 49 of [22, Chapter VII]. We refer the reader to this source for definitions of piping and TRAIL in the compact case and for discussions of these topics.
3.3 THEOREM. Let M be a PL n-manifold, Xx a closed PL subspace of M in ME, n-x$1, T a tree embedded as a closed PL subspace of M in ME, and F:XHIàM a proper PL homotopy such that F(XHI)dME, F0 is the inclusion and F1(X)dT. Then there are closed PL subspaces Yy and Zz of M lying in ME such that XdY`Z with y#x+1 and 0<z#max{2x-n+2,1}.
Proof. If x=m-1 or x=m-2, the conclusion of the theorem follows immediately by letting Y=Z=X. Therefore we assume m-x$3.
Since F is proper, we may triangulate M and XHI so that F is simplicial. We use the homotopy F to obtain g:CF1àM, a proper PL map in general position with g(CF1)dME, g|X the inclusion on X, and g|T the inclusion on T. (See Section 4 of [8] for details.) Let Xx-1 be the (x-1)-skeleton of X and let f=F1|Xx-1:Xx-1àT. We apply a non-compact version of Zeeman's Piping lemma [22, Lemma 48] to the triple Xx, CfxdCF1x+1. We obtain a proper PL map g':CF1àM such that g'(CF1)dME, g'|XxÈCfx=g|XxÈCfx, and a PL subspace J1dCF1x+1 such that
(i) S(g')dJ1 (S(g') is the singular set of g')
(ii) DIM J1#2x-n+2
(iii) DIM(CfÇJ1)#2x-n+1
(iv) CF1`CfÈJ1`Cf.
Define Y=g'(CF1). Then DIM Y#x+1,
Y is closed, YdME, and XdY.
By (i) and (iv), Y=g'(CF1)`g'(CfÈJ1).
Let b be a simplicial collapse applicable to Cf
such that b:Cf`T.
We have Cf`TÈTRAILb(J1ÇCf).
By (i) again, we have Y`g'(CfÈJ1)
and using (i) once more, and the collapse of the last sentence we have
g'(CfÈJ1)`g'(TÈTRAILb(J1ÇCf)ÈJ1).
Let Z=g'(TÈTRAILb(J1ÇCf)ÈJ1).
Since g'(T)dZ and DIM TRAILb(J1ÇCf)#2x-n+2,
then DIM Z#max{2x-n+2,1}, and 0<DIM Z. We
now have XdY`Z,
Z is closed, and ZdME. Note that if x<(n-1)/2, then 2x-n+2<1 so
that DIM J1#0 and DIM TRAILb(J1ÇCf)#0.
Since Y`Z using the collapse of CF1
to T, each component of CF1 contains a
component of T, and T is connected, then CF1 is
connected and Y and Z must be connected. Hence the 0-skeleton of Z, i.e., from J1,
and TRAILb(J1ÇCf),
must be in T, so that Z-g'(T)=T. Thus Y`T. €
We now use Theorem 3.3 to obtain sufficient conditions for a subspace of a manifold to be quasi-trivial. The following is a non-compact analog of [13, Lemma 3].
3.4 THEOREM. Suppose {Mi}i=14 is a sequence of PL n-manifolds such that each Mi is a closed PL subspace of Mi+1 lying in MEi+1, and for i=1, 2, ... there is a tree Ti embedded as a closed PL subspace of Mi+1 and a proper homotopy Fi:MiHIàMi+1 such that Fi(MiHI)dMEi+1, Fi0 is the inclusion on Mi, and Fi1(Mi)dTi. Then if i=1, 2, ... and Xx is a closed PL subspace of with n-x$3, Xx is quasi-trivial in Mi+x+1.
Proof. We begin the inductive proof of the theorem by considering the case x=0. Hence, let i be a positive integer and X be a discrete set of points in Mi. Let f denote Fi|XHI. We may suppose that f is a general position map in general position with respect to Ti. It follows, since DIM(XHI)=DIM Ti=1, DIM Mi+1$3, and F is proper, that F is an embedding and that F(XHI)ÈTi is a PL tree embedded as a closed subspace of Mi+1 lying in MEi+1. Letting C be a regular neighborhood in MEi+1 of F(XHI)ÈTi, then C is a quasi-cell, XdCE and it follows that X is quasi-trivial in Mi+1.
Now suppose, inductively, that the conclusion of the theorem holds for every
positive integer i and for all non-negative integers x#a-1,
where n-(a-1)$4. Consider XadMi,
and let F denote Fi|X. Then
by Theorem 3.3, there exist closed PL subspaces Yy and Zz of Mi+1 lying in
MEi+1 such that XdY`Z
with 0<z#max{2a-n+2,1}.
Then z#2a-n+2=a-(n-a)+2#a-3+2=a-1
or if n=4, a=1, z=1. In the first case, by
the inductive assumption, Z is quasi-trivial in Mi+1+z+1. But
i+1+z+1#i+2+2a-n+2=i+a+1+(a-n+3)#i+a+1.
It follows that Mi+1+z+1dMi+a+1,
and hence, that Z is quasi-trivial in Mi+a+1.
But Y`Z, so Y is quasi-trivial in Mi+a+1
and, since XdY, X is quasi-trivial in Mi+a+1.
This completes the induction and leaves only the special case n=4,
a=1. The last three sentences of the proof
of Theorem 3.3 show how to complete the proof for this case. Since 2a-n+2<1, Y`Z=Ti,
which is quasi-trivial in Mi+1dMi+2.
Thus X is quasi-trivial in Mi+a+1=Mi+2. €
3.5 DEFINITION. Suppose M is a PL n-manifold, XdME and U is a neighborhood of X in M. A sequence of triples {Hi-1,Ti,Fi}i=14 is said to be a quasi-special sequence for X in U provided:
(i) Hi+1 and Ti+1 are closed PL subspaces of M lying in HEi, i=0, 1, 2, ... ,
(ii) Hi-1 is a PL n-manifold with MHi-1¹Æ, and Ti is a tree, i=1, 2, ... ,
(iii) Fi+1:Hi+1HIàM is a proper PL homotopy with Fi+1(Hi+1HI)dHEi, F0i+1 the inclusion on Hi+1, and F1i+1(Hi+1)=Ti+1, i=0, 1, 2, ... ,
(iv) Hi is a closed neighborhood of X, i=1, 2, ... , and X=Çi=14Hi, and
(v) if Y is a closed PL subspace of Hi+1 and DIM Y#n-3, then Y is quasi-trivial in Hi, i=1, 2, ... .
If for each closed neighborhood U of X, there is a quasi-special sequence for X in U, then we say that quasi-special sequences for X in M exist strongly. If there is a quasi-special sequence for X in M and if each quasi-cell N with XdNE there is a quasi-special sequence for X in N, then we say that quasi-special sequences for X in M exist weakly.
3.6 REMARKS. (a) In requirement (iii) we define Fi+1 as
having range M; since the image of Fi+1 is contained in HEi and we shall always be
dealing with situations in which Hi is a closed subspace of M, i=0,
1, ... , we shall often regard Hi as the range of Fi+1.
(b) If quasi-special sequences for a set X in a manifold M
exist strongly, then X must be connected, since each Ti is connected.
The following result connects the notions of quasi-special sequences and the property SUV4.
3.7 THEOREM. Let M be a PL n-manifold, n$3. Then a closed subset X of M lying in ME has SUV4 if and only if quasi-special sequences for X in M exist strongly.
Proof. Suppose quasi-special sequences for X in M exist strongly. We shall show that for each closed neighborhood U of X, there is a PL submanifold V of M, with non-empty boundary, such that XdVEdVdUE, a tree T embedded as a closed PL subset of U in UE, and a proper PL homotopy F:VHIàU with F0 the inclusion on V, F1(V)=T and F(VHI)dUE. It then follows from Theorem 2.10 that X has property SUV4 in M.
Let H0 and H1 be PL submanifolds of M lying in UE, given by the assumption, with F1, T1 the homotopy and tree, respectively for H1 into H0. By Remark 3.6 (b) we may assume that H1 is connected. The required V is H1, the required homotopy is F1 and the tree is F11(H1)=T1.
Suppose X has SUV4. Let ε1, ε2, ... be a sequence of positive real numbers with limi®4 εi=0 and let N(x: εi) be the closed εi-neighborhood of X in M. Let U be a given closed neighborhood of X in M. We shall construct a quasi-special sequence for X in U.
Let V0 be a closed PL manifold neighborhood of X in U. Let U1=V0ÇN(x: ε1) and let V1 be a connected PL submanifold of M with non-empty boundary such that XdVE1dV1dUE1, T1 be a tree embedded as a closed PL subset of U1 in UE1, and G':V1HIàU1dV0 be a proper homotopy with G'0 the inclusion on V1, G'1(V1)=T1' and G'(V1HI)dUE1dVE0.
Let U2=V1ÇN(x: ε2) and choose V2, G2 and T2' as above, where G2(V2HI)dUE2dVE1. Inductively, having obtained Vi, Gi, Ti', define Ui+1=ViÇN(x: εi+1) and choose Vi+1, Gi+1 and Ti+1' as above. The sequence of triples {(Vi-1, Ti', Gi)}i=14 satisfies properties (i) through (iv) of the definition of a quasi-special sequence for X in U. Now let H0=V0 and for i=1, 2, ..., let Hi=V1+i(n-2), Ti=T1+i(n-2)' and Fi=G1+i(n-2)|V1+i(n-2)HI. Then by the comment above and by Theorem 3.4 {(Hi-1, Ti, Fi)}i=14 is a quasi-special sequence for X in U. €
4 QUASI-CELLULARITY.
A closed set X lying in the interior of an n-manifold M is said to be cellular if there exists a sequence {Ci}i=14 of n-cells such that MÉC1ÉCE1ÉC2ÉCE2É ... ÉÇi=14Ci=X. For a summary of results concerning this concept, see [15].
We would like to define an analogous concept which need not require compactness and in which cells are replaced by quasi-cells. Unfortunately, we encounter problems in dealing with such objects which do not occur with cellular sets. One such problem involves the fact that a cellular set is compact; hence in the interior of any neighborhood of the cellular set, there is an n-cell whose interior contains the cellular set. This is not true in general for the nested intersection of quasi-cells.
Suppose X is the x-axis in ú2. Then X is a tree embedded very nicely in ú2. Certainly we would like X to be "quasi-cellular" when this term is defined. If we were given only one sequence of quasi-cells having X as its intersection, we would not know whether of not X has the property of having a quasi-cell neighborhood lying in the interior of any given neighborhood of X. For instance, suppose {Ni}i=14, where Ni={(x, y)0ú2 | |y|#1/i}, is the one given sequence (Figure 4),
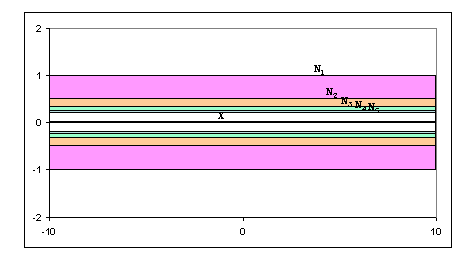
Figure 4. X and {Ni}i=14
and define U={(x, y)0ú2 | |xy|#1 and |y|#1} (Figure 5). Clearly there is no positive integer i so that NidUE. Thus the property of a "quasi-cellular" set having arbitrarily close quasi-cell neighborhoods must be included in the definition if it is to be required.
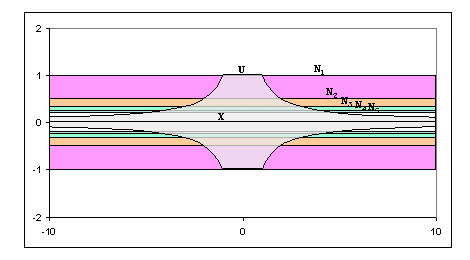
Figure 5. X, {Ni}i=14 and U
4.1 DEFINITION. A closed set X contained in the interior of an n-manifold M is said to be strongly quasi-cellular if for each closed neighborhood U of X, there is a quasi-cell N such that XdNEdNdUE.
4.2 REMARK. It is easily seen that if X is strongly quasi-cellular in an n-manifold M, then X is connected.
We also define a weaker form of "quasi-cellularity."
4.3 DEFINITION. A closed set X contained in the interior of an n-manifold M is said to be weakly quasi-cellular if there exists a sequence of quasi-cells {Ni}i=14, Ni+1dNEi, X=Çi=14Ni, and if for each quasi-cell Q containing X in its interior, there is such a sequence with N1dQE.
4.4 REMARKS. (a) If X is a set contained in the interior of a
topological n-manifold, n$5, and X has SUV4, then some open neighborhood of X has a PL
structure by Kirby and Siebenmann [11]. Since our interest is in "close
neighborhoods" of such sets, we shall assume that if XdMEn, n$5, has SUV4, then M has a PL structure.
(b) If X is a strongly or weakly quasi-cellular set lying in
the interior of a topological n-manifold, n$5, then some neighborhood of X has a PL structure
trivially. As above, if XdMEn, n$5, and X is strongly or weakly quasi-cellular, we
will assume that M has a PL structure.
4.5 THEOREM. Let X be contained in the interior of a PL n-manifold M, n$2. If X is strongly quasi-cellular, then X is weakly quasi-cellular. However, if X is weakly quasi-cellular, it need not be strongly quasi-cellular.
4.6 EXAMPLE. The "topologists' sin 1/x-curve" minus an end point of the "closure line segment," when embedded as a closed subset of ú2dún is weakly quasi-cellular in ún, but not strongly quasi-cellular in ún. In Figure 6, X is the curve (including the heavy closure line, but minus the point p). U is a neighborhood that does not include the elliptical areas in each of the bends of the curve.
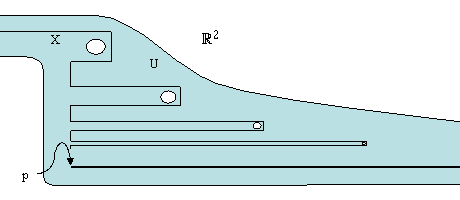
Figure 6. "Topologists' sin 1/x-curve" minus an end point
Figure 7 illustrates the objects that are used in showing that X is weakly quasi-cellular. Each Ti is a tree that coincides with X through the first i bends, then connects with the closure line at the point p. Each Ai is a neighborhood of Ti that also includes the bends of X that aren't in Ti. Each Ai is contained in U through the first i bends, but "bridges" the holes thereafter.

Figure 7. Sketch of logic demonstrating weak quasi-cellularity
The demonstration that X is not strongly quasi-cellular involves using this U and is described in [8].
We will now examine some properties of quasi-cells and strongly and weakly quasi-cellular sets.
4.7 DEFINITION. Suppose X is a compact topological space, YdZdW are topological spaces, and J+ is the space consisting of the positive integers with the discrete topology. A proper map g:XHJ+àY is said to be properly X-inessential in Z if there exists a proper map G:(XHJ+)HIàZ such that for each x in X and j in J+, G(x, j, 0)=g(x, j), and for each j in J+, G|(XH{j})H{1} is a constant map. If, in addition, A is a subset of W and there is a map G as above such that G[(XHJ+)HI]ÇA=f, then we say that g is properly X-inessential in Z missing A.
4.8 LEMMA. Let X be a strongly quasi-cellular set in the n-manifold M. Suppose N1 is a quasi-cell in M containing X in its interior, P is an (n-3)-dimensional polyhedron and g:PHJ+àN1-X is properly P-inessential in N1. Then g is properly P-inessential in N1 missing X.
Proof. Since g:PHJ+àN1 is a proper map and g(PHJ+)ÇX=f, NE1-g(PHJ+) is a neighborhood of X. Thus, since X is strongly quasi-cellular in M, there exists a quasi-cell N2 such that XdNE2dN2dNE1-g(PHJ+). We regard N2 as a piecewise linear manifold and, as such, there exists a closed polyhedral tree TdNE2 such that N2`T.
By hypothesis, there exists a proper homotopy, F1:(PHJ+)HIàN1
such that F10=g and, for each j in J+, F11|PH{j}
is a constant map. Let Y=(F1)-1(NE2) and Y0=YÇ((PHJ+)H{1}).
Then, as an open subset of (PHJ+)HI,
Y has a PL structure and, by the aforementioned properties of F1, Y0
is a closed polyhedral subspace of Y. Also YÇ((PHJ+)H{0})=f.
Let
ε:(PHJ+)HIà(0, 4) be a map and let d:Yà(0, 4) be defined by d(y)=min{ε(y),DIST(y,(PHJ+)HI-Y)},
for all y in Y. Now, using general position we obtain a PL map F':YàNE2 in general position such
that for all y0Y, DIST(F'(y),F1(y))<d(y)
and, for all y0Y0, F'(y)=F1(y). Define the
function F2:(PHJ+)HIàN1
by
:F'(y),
if y0Y
F2 (y)=;
<F1(y), if yÏY.
By our choice of d, F2 is continuous and, we may choose ε so that since DIST(F2(y), F1(y))<ε(y) for all y0(PHJ+)HI, F2 is proper. Also, since YÇ((PHJ+)H{0})=f, F20=F10=g and, since F'|Y0:Y0àN2=F1|Y0, F21|PH{j} is a constant map for all j0J+. Now, by applying a general position argument again (to shift F'(Y) off of T), we may further suppose that F2((PHJ+)HI)ÇT=f. (It is here that the hypothesis DIM P#n-3 is used.)
Let N3 be a regular neighborhood of T in NE2 such that N3ÇF2((PHJ+)HI)=f.
Then, as in the case of compact regular neighborhoods [10, Corollary 2.16.2], it
follows that N2-NE3=Cl(N2-N3)
can be identified with MN2H[0,
1], with MN2H{0}
and MN2 identified. The map
F":Cl(N1-N3)àN1
defined, via this identification, by
:z,
if z0N1-N2
F"(z)=;
<(x,
0), if z=(x,
t)0Cl(N2-N3)
is proper. Thus the map G:(PHJ+)HIàN1
defined by G(x, j, t)=F"(F2(x, j, t)) is proper. It follows readily
that G0=g, G1|PH{j}
is a constant map for all j0J+, and that N2Ç((PHJ+)H{0})=f.
The latter implies that XÇ((PHJ+)H{0})=f
and the proof is complete. €
4.9 REMARK. Suppose XdMEn, n$6, and X is strongly or weakly quasi-cellular. Then we may as well assume that X is strongly or weakly PL quasi-cellular. That is, we may assume that the quasi-cells obtained from the respective definitions are actually piecewise linear subsets of M (cf. Remarks 4.4 (a), (b)). (See the fourth theorem on page 1 of [12].)
4.10 REMARK. It is easily seen that if the image of g and the image of the homotopy F' are in NE1, then the image of G can be required to be in NE1-X.
4.11 DEFINITION. Suppose X is a set contained in the topological space Y. We say that X satisfies the strong quasi-cellularity criterion (in Y), if for each closed neighborhood U of X, there is a closed neighborhood V of X lying in UE such that each proper map g:SkHJ+àV-X which is properly Sk-inessential in V is properly Sk-inessential in U missing X, for k=0 or 1.
4.12 REMARK. (a) McMillan [15, p.3] defines the cellularity
criterion for a compactum X embedded in a space Y as the property that for
each open set U containing X, there is an open set V such that XdVdU
and each loop in V-X is null-homotopic in U-X.
(b) It is easy to see that if X is a compactum with property
UV4 in the normal space Y and satisfying the
strong quasi-cellularity criterion in Y, then X satisfies the cellularity
criterion in Y. To see this, let U be an open set containing X, let U' be a
closed neighborhood of X such that U'dU,
and let V be the closed neighborhood given by the strong quasi-cellularity
criterion for the neighborhood U'. Since X has property UV4 in Y, there exists an open neighborhood W of
X such that XdVE and W is inessential in V. Let
l:S1àW-X
be a loop. Then, since W is inessential in V, l
is null-homotopic in V. Hence, by our choice of V,
l is null-homotopic in U'-X, and hence in U-X.
(c) Suppose X lies in the interior of an n-manifold M, has
SUV4 and satisfies the strong quasi-cellularity
criterion. If U is a neighborhood of X in M, then there is a quasi-special
sequence for X in U {Hi-1,Ti,Fi}i=14
with the null-homotopy property: for each i=0, 1, 2, ... and each proper
map g:SkHJ+àHi+1-X
which is properly Sk-inessential in Hi+1, g is properly Sk-inessential
in Hi missing X, k=0 or 1.
(d) Suppose X is closed and connected and satisfies the
strong quasi-cellularity criterion in the locally path connected space Y and U
is a closed neighborhood of X in Y. Then U-X is path connected if U is path
connected.
(e) It is easy to see that if X is a closed subset of the
space Y having property SUV4 in Y and satisfying the strong
quasi-cellularity criterion in Y, then if U is a simply connected closed
neighborhood of X in Y, U-X is simply connected.
(f) If S={Hi-1,Ti,Fi}i=14
is a quasi-special sequence for a closed subset X of a PL n-manifold, and S has
the null-homotopy property, then there is a subsequence {H'i-1,T'i,F'i}i=14
of S with the additional property that if l
is a loop in H'i+1-X, then is null-homotopic in H'i-X,
and if a:S0àH'i+1-X
is a map, then a is null-homotopic in H'i-X,
for i=1, 2, ... .
4.13 THEOREM. Suppose X is a set contained in the interior of a PL n-manifold, n$4, and X is strongly quasi-cellular in M. Then X has SUV4 and X satisfies the strong quasi-cellularity criterion.
Proof. Let U be a closed neighborhood of X and V a quasi-cell such that XdVEdVdUE. Let V be triangulated so that there is a closed tree T embedded as a subcomplex of V in VE with V as the simplicial neighborhood of T and V`T. This collapse defines a proper PL homotopy H:VHIàU with H0 the inclusion on V, H1(V)=T and H(VHI)dUE. Thus X has SUV4.
Let U be a closed neighborhood of X and V a quasi-cell such that XdVEdVdUE. Let k=0 or 1 and let g:SkHJ+àV-X be a proper map which is properly Sk-inessential in V. By Lemma 4.8, g is properly Sk-inessential in V missing X; hence g is properly Sk-inessential in U missing X; and X satisfies the strong quasi-cellularity criterion in M. €
4.14 THEOREM. Suppose X is a set contained in the interior of a PL n-manifold, n$4, and X is weakly quasi-cellular in M, then quasi-special sequences for X in M exist weakly.
Proof. By the definition of weak quasi-cellularity there is a nested sequence of quasi-cells closing down on X. This satisfies the condition of a quasi-special sequence for X in M existing. For each quasi-cell containing X in its interior, we have such a sequence, and so we also have a quasi-special sequence for X in this quasi-cell. €
4.15 DEFINITION. If X is contained in a manifold M and there is a quasi-special sequence for X in M with the null-homotopy property, and for each quasi-cell Q with X in its interior there is such a quasi-special sequence in Q, then we say that X satisfies the weak quasi-cellularity criterion.
4.16 REMARK. The weak quasi-cellularity criterion subsumes the requirement that quasi-special sequences for X in M exist weakly.
We shall now consider some examples. We mentioned earlier that it seemed fitting that the x-axis in ú2 should be quasi-cellular. Now we can say more.
4.17 EXAMPLE. Any tree T embedded as a closed subcomplex of some locally-finite triangulation of a PL n-manifold M, n$1, is strongly quasi-cellular.
However, not every embedding of a tree in a manifold need be strongly quasi-cellular.
4.18 EXAMPLE. For each n$4, there is an arc embedded in ún which is not strongly quasi-cellular. Let E be a set homeomorphic to [0, 1] in ún, n$3, such that ún-E is not simply connected [3, Theorem 3F]. If E satisfies the strong quasi-cellularity criterion then, by and earlier remark, E satisfies the cellularity criterion, and hence, for n$3 by [15] is cellular, a contradiction. Hence E does not satisfy the strong quasi-cellularity criterion and, by Theorem 4.13, if n$4, E is not strongly quasi-cellular.
4.19 EXAMPLE. For each n$4, there is a closed topological line in
ún which is not strongly quasi-cellular. Let Edún
be the arc of Example 4.18 with
ún-E not simply connected. Since is
ún-1/EHú1
homeomorphic to
ún, [1], then
L=E/EHú1dún-1/EHú1
is a topological line in
ún. To see that
ún-L is not simply connected, we simply note that (ún-1-E)Hú1
is not simply connected. By a previous remark, L does not satisfy the strong
quasi-cellularity criterion in
ún, and hence L is not strongly quasi-cellular in
ún.
We now show that certain pathological sets are strongly quasi-cellular.
4.20 EXAMPLE. For n$4, there is an everywhere wild, non-compact, strongly
quasi-cellular set in
ún. By judicious use of Rushing's theorems and lemmas in [16],
we obtain an everywhere wild (n-3)-dimensional cellular set F in
ún-1 and see that FHú1
is everywhere wild in
ún. Let U be a closed neighborhood of FHú1
in
ún. For each i$0, define
εi>0 so that N(FH[i,
i+1];
εi)dUE and so that for i>j,
εi<εj
and limi®-4
εi=0. Similarly, for each i<0,
define di$0 so that N(FH[i-1,
i]; di)dUE, so that for i>j,
di>dj and limi®-4 di=0. Since F is cellular, define for each i$0, Ni to be an (n-1)-cell so that
NidN(F;
εi)ÇN(F;
d-i)dún-1
and so that for i>j, NidNj.
For i$0, NiH[i,
i+1]ÇNi+1H[i+1,
i+2]=Ni+1, and NiH[-i-1,
-i]ÇNi+1H[-i-2,
-i-1]=Ni+1, we have that Q=Èi=04[NiH[i,
i+1]ÈNiH[-i-1,
-i]] is an n-quasi-cell lying in UE containing X in its interior. (Note
that it is easy to see that Q may be triangulated so that it collapses to pHú1
for some point p in F).
4.21 REMARK. Suppose XdME has property SUV4 and satisfies the strong quasi-cellularity
criterion. Then, if U is a closed neighborhood of X, there exists a closed
neighborhood V of X lying in U such that for every v0V-X, the inclusion-induced homomorphism
i*:π1(V-X,v)àπ1(U-X,v)
is trivial. The converse is not true in general, unless X is compact.
However, the strong quasi-cellularity criterion can be stated in algebraic
terms. E. M. Brown [4] has defined, for non-compact polyhedra K, the groups πm(K,a),
where a:[0, 4)àK
is a proper map. In terms of these groups (when they exist) we can give the
following equivalent statement of the strong quasi-cellularity criterion in the
PL manifold M:
Suppose a polyhedron XdME has property SUV4. Then X satisfies the strong
quasi-cellularity criterion if and only if for each closed neighborhood U of X
there exists a closed polyhedral neighborhood V of X such that
(1) the inclusion induced
homomorphism i*:π1(V-X,v)àπ1(U-X,v)
is trivial for all v0V-X, and (if X is non-compact),
(2) the inclusion induced
homomorphism π1(i):π1(V-X,a)àπ1(U-X,a)
is trivial for all proper maps a:[0, 4)àV
with a([0, 4))dV-X
CONTINUATION: "Quasi-Cellularity Criteria."
REFERENCES
1. Andrews, J. J. and M. L. Curtis, "n-Space Modulo an Arc," Ann. of Math., (2) 75 (1962), 1-7.
2. Ball, B. J. and R. B. Sher, "A Theory of Proper Shape for Locally Compact Metric Spaces," Fund. Math., 86 (1974), 164-192.
3. Blankenship, W. A., "Generalization of a Construction of Antoine," Ann. of Math. (2) 53 (1951), 276-297.
4. Brown, E. M., "Proper Homotopy Theory in Simplicial Complexes," preprint. Possibly published as "On the Proper Homotopy Type of Simplicial Complexes," in Topology Conference, LNmaths 375 (1974) Springer, pp 41-46.
5. Cohen, M. M., "Simplicial Structures and Transverse Cellularity," Ann. of Math. (2) 85 (1967), 218-245.
6. Curtis, M. L. and D. R. McMillan, "Cellularity of Sets in Products," Michigan Math. J. 9 (1962), 299-302.
7. Dugundji, J., Topology, Allyn and Bacon, Inc., (Boston), 1966.
8. Hartley, D. S., III, Quasi-Cellularity in Manifolds, Dissertation, University of Georgia, Athens, GA, 1973 (Ref # A 515428, Dec 27 1973, University Microfilms, 300 North Zeeb Rd, Ann Arbor, MI 48106).
9. Hu, S. T., Theory of Retracts, Wayne State University Press, (Detroit), 1965.
10. Hudson, J. F. P., Piecewise Linear Topology, W. A. Benjamin, Inc., (New York), 1969.
11. Kirby, R. C. and L. C. Siebenmann, "A Triangulation Theorem," Abstract in Notices Amer. Math. Soc. 16 (1969), 433.
12. Kirby, R. C., "Lectures on Triangulations of Manifolds," Mimeographed notes, UCLA.
13. McMillan, D. R. and E. C. Zeeman, "On Contractible Open Manifolds," Proc. Cambridge Philos. Soc. 58 (1962), 221-224.
14. McMillan, D. R., Jr., "A Criterion for Cellularity in a Manifold," Ann. of Math. (2) 79 (1964), 327-337.
15. ___________, "UV Properties and Related Topics," Mimeographed notes.
16. Rushing, T. B., "Everywhere Wild Cells and Spheres," Rocky Mountain J. math. 2 (1972), 249-258.
17. Scott, A., "Infinite Regular Neighborhoods,".J. London Math. Soc. 42 (1967), 245-253.
18. Sher, R. B., "Property SUV4 and Proper Shape Theory," Trans. Amer. Math. Soc. 190 (1974), 345-356.
19. Spanier, E. H., Algebraic Topology, McGraw-Hill Book Company, (San Francisco), 1966.
20. Tatalias, K. D., Unknotting Piecewise Linear Spaces, Dissertation, Univ. of Georgia, 1972.
21. Whitehead, J. H. C., "Simplicial Space, Nuclei and m-Groups," Proc. London Math. Soc. 45 (1939), 243-327.
22. Zeeman, E. C., "Seminar on Combinatorial Topology," I.H.E.S. Paris 1963 (1966), Mimeographed notes.
![]() Return
to Website Entrance Page
Return
to Website Entrance Page