Page Last Updated: Tuesday, 19 January 2016 11:02 EDT, (c) 1973, 2007, 2008, 2016

PUBS: Quasi-Cellularity Criteria

Dean S. Hartley III

Note: If SUV-infinity appears as SUV4, you may not have the font "WP MathA" installed. You may download the WP MathA and WP MathA Extended fonts with control+click on the following links: WPHV06NA.TTF and  WPHV07NA.TTF. (Or you may find them at http://instruct1.cit.cornell.edu/courses/fontfix.htm.) Save the files to your Fonts folder (probably C:\Windows\Fonts). If you cannot save them there, save them somewhere else. Then right click on the file and choose "install." You may have to reboot for these to be applied by Windows.

Abstract. It is demonstrated that a set embedded in a manifold (with certain technical conditions) is strong quasi-cellularity if and only if it has the SUV⁴ property and satisfies a strong quasi-cellularity criterion. Moreover, a locally compact, finite-dimensional metric space has the SUV⁴ property with respect to metric ANRs if and only if it embeds as a strongly quasi-cellular subset of some (high dimensional) manifold. In like manner, a set embedded in an n-manifold (with technical conditions) is weakly quasi-cellular if it satisfies a weak quasi-cellularity criterion.

This research is a condensation of the second half of the author's Ph.D. dissertation, written at the University of Georgia under the direction of Professor R. B. Sher.  I would like to express my thanks to Professor Sher for his aid.  His advice and criticism have been invaluable.

AMS 1970 Subject Classifications. Primary 57A60, 57C99; Secondary 57C30, 57C40.
MSC 2000 Subject Classifications. Primary 57N60, 57Q99; Secondary 57Q30, 57Q40, 57Q65.

Key words and phrases. Cellular, cellularity criterion, properly S^k-inessential, quasi-cell, quasi-cellular, quasi-cellularity criterion, quasi-trivial, strong quasi-cellularity criterion, strongly quasi-cellular, SUV⁴, tree, UV⁴, weak quasi-cellularity criterion, weakly quasi-cellular.

NOTATION

UE and Int(U) symbolize the topological interior of U.
ME_i+1 symbolizes the topological interior of M_i+1 (the apparent sequence of the superscript and subscripts is purely an artifact of the HTML).
( €_i)_i=1⁴ symbolizes an operation or group of indexed entities ranging from the index of 1 to the index of 4 (the apparent sequence of the superscript and subscripts is purely an artifact of the HTML).
J⁺ symbolizes the set of positive integers.
ú¹ symbolizes the real number line.
Sⁿ symbolizes the Euclidean n-sphere.
Mⁿ and X^x symbolize n-dimensional and x-dimensional objects, respectively.
Fⁱ and Gⁱ, where F and G are maps, symbolize indexed maps, not n-dimensional objects.
F₀ and F₁, where F is a homotopy, F:XHIàY, symbolize F(X,0) and F(X,1), respectively.
MB symbolizes the boundary of B.
-->> symbolizes an onto map.
Cl(X) symbolizes the topological closure of X.
K symbolizes the complex closure of K.
FY symbolizes the Freudenthal compactification of a space Y.
EY symbolizes the set of ends of Y.
` symbolizes a collapse.

1 INTRODUCTION.

In this work we show that our extensions of cellularity [5] were the correct ones in that we are able to prove McMillan type theorems [8 Theorem 1] for strong quasi-cellularity and for weak quasi-cellularity. In fact, our extension of UV⁴ to SUV⁴ shows an even closer analogy to the compact case. McMillan remarks [9, p 21] that, for finite dimensional continua X, X0UV⁴ if and only if X has cellular embeddings into some (high dimensional) Euclidean space. We show in Theorem 3.12 that, for locally compact, finite dimensional metric spaces X, X0SUV⁴ if and only if X has a strongly quasi-cellular embedding into some (high dimensional) manifold. B. J. Ball and R. B. Sher have developed a theory of proper shape [1] and Sher has used this [13, Theorem 3.1] to show that, for X a locally compact metrizable space, X0SUV⁴ if and only if X has the proper shape of a tree.

The work below comes from the second half of [6]; however, there is additional background material in the Appendix of [6] that is not included. This material includes proofs on infinite regular neighborhoods, proper maps, mapping cylinders, general position, and engulfing theorems. Some of the material on engulfing theorems is repeated in section 5, below.

2 PRELIMINARY DEFINITIONS AND NOTATION.

We wish to recall some definitions and notation from [5] for the reader's convenience.

We will continue to use cl(K) to mean the topological closure of a set K and K to mean the complex closure, that is the smallest complex containing K.  We will continue to use Dugundji [4] and Hudson [7] for general background material and most of the spaces we deal with will be assumed to be locally compact metric spaces.

2.1 DEFINITION. A map f:XàY of topological spaces is proper if f ^-l(C) is compact whenever C is compact.

2.2 DEFINITION. A tree is a connected, simply connected, locally-finite l-complex.

2.3 DEFINITION. Suppose N is an n-manifold. If there is a PL n-manifold N'dEⁿ which is a closed regular neighborhood of some tree, and if there is a homeomorphism h from N' onto N, then N is called an n-quasi-cell. If the dimension is obvious, or not relevant, N will be referred to simply as a quasi-cell.

2.4 DEFINITION. Suppose X is a compact topological space, YdZdW are topological spaces, and J⁺ is the space consisting of the positive integers with the discrete topology. A proper map g:XHJ⁺àY is said to be properly X-inessential in Z if there exists a proper map G:(XHJ⁺)HIàZ such that for each x in X and j in J⁺, G(x, j, 0)=g(x, j), and for each j in J⁺, G|(XH{j})H{1} is a constant map. If, in addition, A is a subset of W and there is a map G as above such that G[(XHJ⁺)HI]ÇA=f, then we say that g is properly X-inessential in Z missing A.

2.5.1 DEFINITION. A set X contained in the interior of an n-manifold is said to be quasi-trivial in M if X is contained in a quasi-cell in ME.

2.5 DEFINITION. Suppose M is a PL n-manifold, XdME and U is a neighborhood of X in M. A sequence of triples {H_i-1,T_i,Fⁱ}_i=1⁴ is said to be a quasi-special sequence for X in U provided:

        (i)    H_i+1 and T_i+1 are closed PL subspaces of M lying in HE_i, i=0, 1, 2, ... ,

        (ii)   H_i-1 is a PL n-manifold with MH_i-1¹f, and T_i is a tree, i=1, 2, ... ,

        (iii)  Fⁱ⁺¹:H_i+1HIàM is a proper PL homotopy with Fⁱ⁺¹(H_i+1HI)dHE_i, F₀ⁱ⁺¹ the inclusion on H_i+1, and F₁ⁱ⁺¹(H_i+1)=T_i+1, i=0, 1, 2, ... ,

        (iv)  H_i is a closed neighborhood of X, i=1, 2, ... , and X=Ç_i=1⁴H_i, and

        (v)   if Y is a closed PL subspace of H_i+1 and DIM Y#n-3, then Y is quasi-trivial in H_i, i=1, 2, ... .

If for each closed neighborhood U of X, there is a quasi-special sequence for X in U, then we say that quasi-special sequences for X in M exist strongly. If there is a quasi-special sequence for X in M and if each quasi-cell N with XdNE there is a quasi-special sequence for X in N, then we say that quasi-special sequences for X in M exist weakly. We say that {H_i-1,T_i,Fⁱ}_i=1⁴ has the null-homotopy property if for each i=0, 1, 2, ... and each proper map g:S^kHJ⁺àH_i+1-X which is properly S^k-inessential in H_i+1, g is properly S^k-inessential in H_i missing X, k=0 or 1.

2.6 DEFINITION. Suppose M is a topological space and X is a subset of M. If, for each closed neighborhood U of X, there is a closed neighborhood V of X contained in UE, a tree T, a map f:VàT, a proper map g:TàU, and a proper homotopy H:VHIàU such that H₀ is the inclusion and H_l =gBf, the we say that X has the strong UV⁴ property in M; this being the case, we say that X has property SUV⁴ in M.

The following theorem [5, Theorem 2.10] gives an equivalent definition for the case that M is a PL n-manifold, n$3.

2.7 THEOREM. Suppose M is a PL n-manifold, n$3, and X is a closed subset of M lying in ME. Then X has SUV⁴ in M if and only if for each closed neighborhood U of X, there is a PL submanifold V, with a non-empty boundary, such that XdVEdVdUE, a tree T embedded as a closed PL subset of M in UE, and a proper PL homotopy H:VHIàU with H₀ the inclusion, H₁(V)=T and H(VHI)dUE.

We will also use the following theorem [5, Theorem 3.7].

2.8 THEOREM. Let M be a PL n-manifold, n$3. Then a closed subset X of M lying in ME has SUV⁴ if and only if quasi-special sequences for X in M exist strongly.

2.9 DEFINITION. Suppose X is a set contained in the topological space Y. We say that X satisfies the strong quasi-cellularity criterion (in Y), if for each closed neighborhood U of X, there is a closed neighborhood V of X lying in UE such that each proper map g:S^kHJ⁺àV-X which is properly S^k-inessential in V is properly S^k-inessential in U missing X, for k=0 or 1.

2.10 DEFINITION. If X is contained in a manifold M and there is a quasi-special sequence for X in M with the null-homotopy property, and for each quasi-cell Q with X in its interior there is such a quasi-special sequence in Q, then we say that X satisfies the weak quasi-cellularity criterion.

3 STRONG QUASI-CELLULARITY AND SUV⁴.

3.1 LEMMA. Suppose X is a closed subset of a PL n-manifold M, X lies in ME and DIM X#n-1. Further suppose that V is a closed neighborhood of X in M and g:J⁺àV is a proper map. Then there exists a proper map G:J⁺HIàV such that G₀=g and G(i,1)ÏX, for all i0J⁺.

Proof. Clearly, we may suppose that for each i0J⁺, g(i)0VE; for otherwise, we would simply define G on these points which are not carried into VE to be the constant homotopy. Let {e_i}_i=1⁴ be a sequence of positive numbers converging to zero. For each i0J⁺, let N_idVE be a PL n-ball whose interior contains g(i) and whose diameter is less than e_i. Since DIM X#n-1, NE_iÇ(V-X)¹f, for all i0J⁺. Since NE_i is arc-connected, there exists a path a_i:[0,1]àNE_i such that a_i(0)=g(i) and a_i(1)0V-X. Then, since g is proper and {e_i}_i=1⁴®0, the map G:J⁺HIàV defined by G(i,t)=a_i(t) is proper. Since G₀=g and G(i,1)=a_i(1)0V-X, this completes the proof. €

3.2 LEMMA. Suppose that U is a locally compact topological space, VdU, T is a tree embedded as a closed subset of U, and F:VHIàU is a proper map such that F₀ the inclusion and F₁(V)=T. Then, if P is a compact, connected space and g:PHJ⁺àV is a proper map, g is properly P-inessential in U.

Proof. We shall define a proper map H:(PHJ⁺)HIàV such that H₀=g and, for each j0J⁺, H₁|PH{j} is a constant map. We first define G on (PHJ⁺)H[0, 1/2] by G_t=F_2tBg, for t0[0, 1/2]. Since P is compact and connected, G_1/2(PH{j}) is a compact subtree of T, for each j0J⁺, and as such is contractible. Thus we have that the map G_1/2|PH{j} is homotopic to a constant map in G_1/2(PH{j}). We shall call this homotopy r^j, with r₀^j=G_1/2|PH{j}. Let R:(PHJ⁺)H[1/2, 1]àT be the map defined by R_t|PH{j}=r_2t-1^j, for t0[1/2, 1]. We note that for each j0J⁺, the set {k|G_1/2(PH{j})ÇG_1/2(PH{k})¹f} is finite. It follows from this that R is proper. Since R_1/2=G_1/2, we may define H:(PHJ⁺)HIàU by H_t=G_t, t0[0, 1/2] and H_t=G_t, t0[1/2, 1]. Since H is proper, H₀=g, and H₁|PH{j} is a constant map, for each j0J⁺, then we are through. €

3.3 DEFINITION. Suppose M is a PL n-manifold, V is a given open set in M, and U is a given closed set in M containing M-V in its interior. Let P denote an arbitrary closed k-dimensional PL subspace of M, and Q a closed PL subspace of P with QdV. We say locally finite k-complexes in M can be pulled into V in U if for each such P and Q there is a proper homotopy H:PH[0, 1]àM such that H₀ is the inclusion on P, H₁(P)dV, H_t is the inclusion on QÈ[(M-U)ÇP] for each t0[0, 1], H(P-QÇUH[0, 1]dU, and there is a map d:Pà(0, 4) with DIST(H₁(p), M-V)>d(p), for each point p0P.

3.4 LEMMA. Let M be a PL n-manifold and let X be a closed, connected subset of ME with DIM X#n-1. Let U be a closed neighborhood of X in M such that a quasi-special sequence for X in U with the null-homotopy property exists. Then locally finite 2-complexes in M can be pulled into M-X in U.

Proof. We first note that [M-(M-X)]dUE, so that the conclusion makes sense according to the definition. Now let P be any closed 2-dimensional PL subspace of M and Q be any closed PL subspace of P in M-X.

Let {H_i-1,T_i,Fⁱ}_i=1⁴ be a quasi-special sequence for X in U with the null-homotopy property. Since X is connected, we may assume that each H_i is connected. We shall only be concerned with the first five manifolds, H₀, H₁, H₂, H₃, and H₄. Let R be a triangulation of M with P, Q and H_i, i=0, 1, 2, 3, 4, triangulated as subcomplexes of R.

We wish to produce a proper homotopy G:PH[0, 1]àM such that G₀ is the inclusion on P, G₁(P)dM-X, G_t is the inclusion on QÈ[(M-U)ÇP] for each t0[0, 1], G(P-QÇUH[0, 1]dU, and so that there is a map d:Pà(0, 4) with DIST(G₁(p), X)>d(p), for each point p0P. We will define G
    (a) on (the vertices of P)H[0, 1],
    (b) on (the 1-simplexes of P)H[0, 1], and
    (c) on (the 2-simplexes of P)H[0, 1].

(a) Let V={v₁, v₂, v₃, ...} be the set of vertices of P. We define G:VHIàM by defining G(v_i, t)=v_i, for all t0[0, 1], if v_i is a vertex of R-H₄ÈQ. Let {v^~₁, v^~₂, v^~₃, ...} be the set of vertices of P not in R-H₄ÈQ. Define g:J⁺àH₃ by g(j)=v^~_j. Lemma 3.1 gives us a proper map G:J⁺HIàH₄ such that G₀=g and G(i, 1)ÏX, for all i0J⁺. We define G(v^~_i, t)=G(i, t), for all i0J⁺.

(b) Let S={s₁, s₂, s₃, ...} be the set of 1-simplexes of P. We define G:SHIàM by defining G(x, t)=x, for all t0[0, 1] and x0s_i if s_i0R-H₄ÈQ. Note that if s_i0R-H₄ÈQ, then so are its vertices, so that G, here defined, agrees with its definition on VHI. Let {s^~₁, s^~₂, s^~₃, ...} be the 1-simplexes of P not in R-H₄ÈQ. Define G₀|s^~_i to be the inclusion on s^~_i, for each i0J⁺. Now for each i0J⁺, Ms^~_i is a pair of vertices, and G(Ms^~_iH{1})dH₄-X. For each i0J⁺, let h_i be a homeomorphism from S⁰ onto Ms^~_i. Define F:S⁰HJ⁺àH₄ by F(z, i)=G(h_i(z), 1). Then since G(s^~_iH{0}ÈMs^~_iH[0, 1])dH₄ and G is proper, F is properly S⁰-inessential in H₄. By the null-homotopy property, F is properly S⁰-inessential in H₃ missing X. It follows from this that G can be properly extended to (È_i=1⁴s^~_i)H{1}, where the extension carries (È_i=1⁴s^~_i)H[0, 1] into H₃-X. In a natural way (cf. the construction of F above), G determines a proper map S¹HJ⁺ from into H₃. Since S¹ is compact and connected, such a map is properly S¹-inessential in H₂ by Lemma 3.2. It follows from this that we may properly extend G to È_i=1⁴(s^~_iH[0, 1]), where the extension carries È_i=1⁴(s^~_iH[0, 1]) into H₂.

(c) Let T={t₁, t₂, t₃, ...} be the set of 2-simplexes of P. We define G:THIàM by defining G(x, t)=x, for all t0[0, 1] and x0t_i if t_i0R-H₄ÈQ. Note that if t_i0R-H₄ÈQ, then so are the 1-simplexes and vertices which are its faces, so that G, here defined, agrees with its definition on SHI. Let {t^~₁, t^~₂, t^~₃, ...} be the 2-simplexes of P not in R-H₄ÈQ. Define G₀|t^~_i to be the inclusion on t^~_i, for each i0J⁺. Now for each i0J⁺, Mt^~_i is identifiable with S¹ and G(Mt^~_iH{1})dH₃-X. In a natural way (cf. the construction of F above), G determines a proper map S¹HJ⁺ from into H₃-X which is properly S¹-inessential in H₂. By the null-homotopy property, this map is properly S¹-inessential in H₁ missing X. It follows from this that G can be properly extended to (È_i=1⁴t^~_i)H{1}, where the extension carries (È_i=1⁴t^~_i)H[0, 1] into H₁-X. We now have the proper map G defined on È_i=1⁴M(t^~_iH[0, 1]). In a natural way again, G determines a proper map S²HJ⁺ from into H₁. Since S² is compact and connected, such a map is properly S²-inessential in H₀ by Lemma 3.2. It follows from this that we may properly extend G to È_i=1⁴(t^~_iH[0, 1]), where the extension carries È_i=1⁴(t^~_iH[0, 1]) into H₀.

We now have our desired homotopy G:PH[0, 1]àM such that G₀ is the inclusion on P, G₁(P)dM-X, G_t is the inclusion on QÈ[(M-U)ÇP] for each t0[0, 1], and G(P-QÇUH[0, 1]dU. Since X is closed and G is continuous, we may define a map d:Pà(0, 4) with DIST(G₁(p), X)>d(p), for each point p0P. €

The properties we are concerned with are topological in nature. We do, however, use a metric defined on whichever manifold is our ambient space. Some of our proofs (e.g., the following lemma and many of the results of Section 4) will require certain properties of that metric which are not available for every metric which might be defined on our manifold. One property we sometimes require is that the closed e-ball, e>0, about a point in the manifold be compact. This means that if a closed subset is non-compact, it has infinite diameter. We have this, for example, if the metric for the manifold is complete [4, Chapter XIV, Theorem 2.3]. Requiring that the metric for our manifold be complete is not a great restriction, since every locally compact metric space has a complete metric [4, Chapter XIV, Corollary 2.4]. We shall henceforth assume that our manifolds are equipped with such metrics.

3.5 DEFINITION. We say that a space Y is k-ULC at the closed subset X, if for each e>0, there is a d>0 such that for each point x0X and map g:S^kàN(x; d), g is e-null-homotopic in Y.

3.6 DEFINITION. Let (M, r) be a metric space with P and U subspaces. We say that P tends to U if given e>0, there is a compact subset CdP such that r(x, U)<e, for each x0P-C.

The following lemma is analogous to Lemma 3.1 with the requirement that X be (n-1)-dimensional replaced by X tends to M-X and M is 0-ULC at X. It is easy to see that if X is (n-1)-dimensional, then X tends to M-X and M is 0-ULC at X.

3.7 LEMMA. Suppose X is a closed subset of a PL n-manifold M, X lies in ME, X tends to M-X and M is 0-ULC at X. If V is a closed neighborhood of X in M and g:J⁺àV is a proper map, then there exists a proper map G:J⁺HIàV such that G₀=g and G(i,1)ÏX, for all i0J⁺.

Proof. We write M as an expanding union of compact sets
    C₁dCE₂dC₂dCE₃d ... dÈ_i=1⁴C_i=M
where C₁ is chose arbitrarily and, for i>1, C_i is chose inductively by the following method. Suppose C_i-1 has been chosen. Using the 0-ULC condition of the hypothesis, let d_i>0 be such that both d_i<1/i and such that for each point x0X, any map g:S⁰àN(x; d) is (1/i)-null-homotopic. Now choose C_i so large that if xÏC_i, then DIST(x, C_i-1)>1 and, using the hypothesis that X tends to M-X, so large that if xÏC_i, then N(x; d_i)ÇM-X¹f.

Now consider the proper map g:J⁺àV. If g(j)ÏX, for some j0J⁺, we let G(j, t)=g(j), for all t0[0, 1]. Thus, for the rest of the argument, we assume that g(j)0X.

If j is such that g(j)0C₂, pick p_j0V-X so that p_j is in the component of V containing g(j). Define G|jH[0, 1]:jH[0, 1]àV so that G₀(j)=g(j) and G₁(j)=p_j.

For i>1, let j0J⁺ be such that g(j)0C_i+1-C_i. Since g(j)ÏC_i, there is a point p_j in (M-X)ÇN(g(j); d_i). By the 0-ULC condition, we may define G^~j:jH[0, 1]àN(g(j); d_i) so that G^~j₀(j)=g(j) and G^~j₁(j)=p_j. Since g(j)ÏC_i, then DIST(g(j), C_i-1)>1; and since d_i<1/i<1, we have G^~j(jH[0, 1])ÇC_i-1=f. We now let q_j be the right hand endpoint of the component of (G^~j)^-1(X) containing (j,0). (We regard {j}H[0, 1] as running from left to right, with (j,0) on the left.) Since G^~j is continuous and V is a neighborhood of X, there is a neighborhood of q_j in {j}H[0, 1] contained in (G^~j)^-1(V). Let r_j be a point in this neighborhood not in (G^~j)^-1(X). Define G^j:jH[0, 1]àV by G^j(j,t)=G^~j(j,t^.r_j).

We now define the map G:J⁺HIàV such that G|{j}H[0, 1]=G^j. It follows that G₀=g and G(j,1)ÏX, for all j0J⁺. To see that G is proper, let C be a compact subset of M. then let C_i be such that CdC_i. Since g is proper, the subset of J⁺, K=G^-1(C_i+1), is finite. Since G has been constructed so that for jÏK, G(jH[0, 1])ÇC_i=f, then for j0K, G(jH[0, 1])ÇC=f. Thus G^-1(C) is compact, G is proper, and the argument is complete. €

The following lemma is the analog of Lemma 3.4, just as the previous lemma was the analog of Lemma 3.1. Also, just as was the case for the previous lemma and Lemma 3.1, the following lemma subsumes Lemma 3.4.

3.8 LEMMA. Let M be a PL n-manifold and let X be a closed, connected subset of ME such that X tends to M-X and M is 0-ULC at X. Let U be a closed neighborhood of X in M such that a quasi-special sequence for X in U with the null-homotopy property exists. Then locally finite 2-complexes in M can be pulled into M-X in U.

Proof. The proof is the same as that of Lemma 3.4, except that where in the proof of Lemma 3.4 an appeal to Lemma 3.1 is made, here the appeal is made to Lemma 3.7. €

We now state and prove our main theorem.

3.9 THEOREM. Let M be a PL n-manifold, n$6, and let X be a closed, connected subset of ME such that M is 0-ULC at X and X tends to M-X. Then, X is strongly quasi-cellular if and only if X has SUV⁴ and satisfies the strong quasi-cellularity criterion.

Proof. The proof of necessity is given by [5, Theorem 4.13].

We will now show the sufficiency of the conditions. For each closed neighborhood U of X, we must find a quasi-cell N such that XdNEdNdUE.

Let H₀ and H₁ be the first two manifolds of a quasi-special sequence for X in U with the null-homotopy property. Let R be a triangulation of M with H₀ and H₁ as subcomplexes. Let R² be the 2-skeleton of R. We use H₁ as the U of Lemma 3.8 to obtain a proper homotopy G:R²H[0, 1]àM such that G₀ is the inclusion on R², G₁(R²)dM-X, G_t is the inclusion on (M-H₁)ÇR² for each t0[0, 1], G(R²ÇH₁H[0, 1])dH₁, and so that there is a map d:R²à(0, 4) with DIST(G₁(p), X)>d(p), for each p0R². If we let {A_p} be {G(pH[0, 1])} for all points p in 2-complexes in M and all homotopies G pulling these 2-complexes into M-X in H₂, we see that we may apply the Infinite Radial Engulfing Theorem (5.2, below) to obtain an engulfing isotopy G':MH[0, 1]àM such that G'₀ is the identity, G'_t|R²ÇH₁=1|R²ÇH₁, R²dG'₁(M-X), and G'_t|cl(M-H₁)=1|cl(M-H₁). This last result is achievable since G moves no point which is in cl(M-H₁) and moves no point into cl(M-H₁) from HE₁ and since G' is picked so that points are moved close to the movement of points by G.

Now define K to equal R²ÇH₁dG'₁(M-X)ÇG'₁(H₁) which equals G'₁(H₁-X). Let L be the complementary complex of K in H₁. Since DIM L#n-3, there is a quasi-cell N* in HE₀ with LdNE*, by the definition of quasi-special sequences. Since G'₁(X) does not intersect K, there is an ambient isotopy, fixed outside of H₀, G":MH[0, 1]àM which pushes N* along the join structure from L to K far enough so that G'₁(X)dG"₁(NE*). Define N=(G'₁)^-1BG"₁(N*). Then XdNEdNdHE₀dUE, and the proof is complete. €

3.10 REMARK. Not every set having SUV⁴ is quasi-cellular as shown by [5, Example 4.19]. However, the following shows that if X is a locally compact, finite dimensional metric space with SUV⁴ (with respect to metric ANRs), then X embeds in some Euclidean space as a strongly quasi-cellular set.

3.11 THEOREM. If X is a closed subset of Eⁿ with SUV⁴, then X is strongly quasi-cellular in Eⁿ⁺³, for n$3.

Proof. Since n+3$6, since DIM X<n+3 supplies that X tends to Eⁿ⁺³-X and Eⁿ⁺³ is 0-ULC at X, and since SUV⁴ is a topological property, so that X has SUV⁴ in Eⁿ⁺³, Then Theorem 3.9 shows that we need only demonstrate that X satisfies the strong quasi-cellularity criterion to have that X is strongly quasi-cellular.

Suppose that U is a closed neighborhood of X in Eⁿ⁺³. Let V be any closed neighborhood of X in Eⁿ⁺³ lying in UE. Now let g:S^kHJ⁺àV-X be a map such that there is a proper homotopy G:(S^kHJ⁺)HIàV with G₀=g and G₁|S^kH{j} a constant map, for j0J⁺ and k=0 or 1. We may suppose, without loss of generality, that G is in general position with respect to Eⁿ. Thus, since DIM(G[S^kHJ⁺HI])#2, then EⁿÇG[S^kHJ⁺HI]=f. Thus g is properly S^k-inessential in U missing X, k=0 or 1, and the proof is complete. €

3.12 COROLLARY. Suppose X is a locally compact, finite dimensional, metric space. Then X has SUV⁴ with respect to metric ANRs if and only if X embeds as a strongly quasi-cellular subset of some PL n-manifold, n$6.

Proof. Since X is a locally compact, finite dimensional metric space, it embeds in Eⁿ, for some n$3. Theorem 3.11 thus completes the proof in one direction. [5, Theorem 4.13] completes the proof for the other direction. €

We now state the following theorem of R. B. Sher [13, Theorem 3.1] to complete the analogy with the compact case mentioned in the introduction (Sh_p is the proper shape function).

3.13 THEOREM. Suppose X is a locally compact metrizable space. Then X0SUV⁴ if and only if there exists a tree T such that Sh_pX=Sh_pT.

4 STRONG QUASI-CELLULARITY AND WEAK QUASI-CELLULARITY.

In section 3 we presented one McMillan type theorem connecting strong quasi-cellularity with SUV⁴ and the strong quasi-cellularity criterion. Our use of the Infinite Radial Engulfing Theorem required certain technical conditions. Rushing [11] has other infinite engulfing theorems which yield similar theorems with other technical conditions. We state these here. We also give McMillan type theorems (of one direction only) for weak quasi-cellularity.

4.1 DEFINITION. Let M be a PL manifold and U an open subset of M. Then we say that (M, U) is p-connected if and only if for each integer i, 0 £ i £ p, and each map
    f:(Dⁱ, MDⁱ)à(M, U)
there exists a homotopy
    F:(Dⁱ, MDⁱ)HIà(M, U)
such that for each t0[0, 1], F_t is a map of the pair (Dⁱ, MDⁱ) into the pair (M, U), F₀=f, and F₁(Dⁱ)dU.

4.2 DEFINITION. We call a manifold M uniformly locally p-connected, p-ULC, if given e>0, there is a d>0 for which every map f:S^pàM such that the diameter of f(S^p) is less than d is e-null-homotopic. If M is p-ULC for 0 £ p £ k, the we say M is ULC^k.

4.3 DEFINITION. Let M be a PL n-manifold, n$2. A set XdME is said to thin down in M, if for each locally finite triangulation R of M, the 2-skeleton R² of R tends to M-X.

4.4 LEMMA. Suppose M is a PL n-manifold, n$2. Then a Set XdME tends to M-X if and only if X thins down in M.

Proof. Suppose X tends to M-X and R is any locally finite triangulation of M. We shall show that R² tends to M-X. Let e>0 be given. Then there is a compact set C such that if x is a point of X-C, then DIST (x, M-X)<e. Now let p be a point of R²-C. If p0X, we have p0X-C, so DIST (p, M-X)<e. If pÏX, then p0M-X, so that DIST (p, M-X)=0.

Suppose X thins down in M. Let e>0 be given. Let R be a locally finite triangulation of M so that MESH R<e/2. Let C be a compact set such that if p0R²-C, then DIST (p, M-X)<e/2. Let C' be the smallest subcomplex of R containing C and let C" be the closed star of C' in R. It is clear that C" is compact. Let x be a point of X-C" and let Q be the set {q|q0R² and DIST(x, q)<e/2}. Now Q is not empty since there is a simplex s in R with x in the interior (rel s) of s, and since the diameter of s is less than e/2, then sÇR²dQ. Also, there is a point p in Q with p0R²-C', for if x0sE and (sÇR²)dC', then s must be in C", but xÏC". Now R²-CÉR²-C', so that if p0R²-C and DIST (p, M-X)<e/2, we have DIST (x, M-X)<e. €

4.5 THEOREM. Let M be a PL n-manifold, n$5, and let X be a subset of ME which tends to M-X. Suppose that for each open neighborhood U of X there is an open neighborhood V of X lying in U such that V is ULC² and V-X is ULC¹. Then X is strongly quasi-cellular if and only if X is closed, has SUV⁴ and satisfies the strong quasi-cellularity criterion.

Proof. The proof of necessity is given by [5, Theorem 4.13].

Suppose then that XdME is closed, has property SUV⁴ in M, and satisfies the strong quasi-cellularity criterion. Let U be any closed neighborhood of X. Let H_i, i=1, 2, 3, 4, and 5, be connected PL submanifolds of M so that
    (1) XdHE_i+1dH_i+1dHE_idH_i-UE, i=1, 2, 3, or 4,
    (2) there exists a proper PL homotopy Fⁱ⁺¹:H_i+1H[0, 1]àH_i, with F₀ⁱ⁺¹ the inclusion, Fⁱ⁺¹(H_i+1H[0, 1])dHE_i, and F₁ⁱ⁺¹(H_i+1)=T_i+1 a closed tree, i=1, 2, 3, or 4,
    (3) MH_i¹f, i=1, 2, 3, 4, or 5,
    (4) if YdH_i+1 is a polyhedron and DIM Y£n-3, then Y is quasi-trivial in H_i, i=1, 2, 3, or 4,
    (5) each map g:S^kàH_i+1-X is null-homotopic in HE_i-X, i=1, 2, 3, or 4, and k=0 or 1. This last condition derives from the strong quasi-cellularity criterion [5, Remark 4.12 (f)].

Let R be a locally finite triangulation of M with H_i i=1, 2, 3, 4, or 5, as subcomplexes and let R² be the 2-skeleton of R. By Lemma 4.4 we know that R² tends to M-X.

Let V be an open subset of HE₅ such that XdV, V is ULC², and V-X is ULC¹. Using the first of Rushing's infinite engulfing theorems (Theorem 5.4, below). Let e'_t:VH[0, 1]àV be an ambient isotopy which extends by the identity to all of M, for which e'₁(M-X) contains all of R² except some compact subset contained in e'₁(V)=V. Let L be a compact subcomplex of R² which contains R²Çe'₁(X) and such that R²-Lde'₁(M-X).

We now wish to apply Stallings' Engulfing Theorem with (L, HE₂Ç(R²-L), e'₁(HE₂-X), HE₂) replacing (P, Q, U, M) (see Theorem 5.3, below, for the variation of the theorem used here). We must show that the pair p=(HE₂, HE₂-X)»(e'₁(HE₂), e'₁(HE₂-X))=(HE₂, e'₁(HE₂-X)) is 2-connected.

Since H₅ is arc connected, if
    f:(D⁰, MD⁰)à(HE₂, HE₂-X)
is a map, with f(D⁰)dX, then there is an arc in H₅ from f(D⁰) to a point in H₅-X. Thus p is 0-connected.

Now consider any map
    f:(D¹, MD¹)à(HE₂, HE₂-X).
Suppose f(D¹)dH₅. Since f( MD¹) is a pair of points in H₅-X, there is a map g:D¹àHE₄-X with g|MD¹=f|MD¹. Since F₁⁴[f(D¹)Èg(D¹)] is a continuum in T₄, f is homotopic (rel MD¹) in HE₃ to g. In the general case, cover f^-1(X) with a finite number of disjoint arcs s₁, s₂, s₃, ... s_k so close to f^-1(X) that each f(s_i)dH₅. By the special case f|s_i is homotopic (rel Ms_i) in HE₃ to a path in HE₄-X. Putting these homotopies together, we see that f is homotopic (rel [D¹-È_i=1^ksE_i]) in HE₂ to a path in HE₂-X. so p is 1-connected.

Now consider any map
    f:(D², MD²)à(HE₂, HE₂-X).
Suppose f(MD²)dH₄-X and f(D²)dH₃. Then we have a map g:D²àHE₃-X with g|MD²=f|MD². Since F₁³[f(D²)Èg(D²)] is a continuum in T₃, f is homotopic (rel MD²) in HE₂ to g. In the general case, cover f^-1(X) with the interiors of a finite number of punctured polyhedral 2-cells, t₁, t₂, t₃, ... t_m which do not meet MD² and such that to f(t_i)dH₅, i=1,2, ...m. Let S be a triangulation of D² so that the t_is are subcomplexes of S. Let A=È_i=1^m(1-skeleton t_i) and let B=D²-È_i=1^mtE_i. By the 0-connectivity of H₅, we have a homotopy (rel M(È_i=1^mt_i)), (since f^-1(X)dINT(È_i=1^mt_i)) of the 0-skeleton of A in H₅ to H₅-X. We use the homotopy extension property for polyhedral pairs [14, Corollary 5, p. 118] to obtain a homotopy from AH[0, 1] into H₅ with the restriction to the 0-skeleton agreeing with the original homotopy. We now use the special case of the proof of the 1-connectivity of , (since the 0-skeleton of AH{1} is carried into H₅-X), to obtain a homotopy φ:AH[0, 1]àHE₃ such that φ₀=f|A, φ₁(A)dHE₄-X and φ_t|AÇB=f|AÇB (AÇB=M(È_i=1^mt_i)). Using the homotopy extension property again, we extend φ to Φ:(È_i=1^mt_i)HI with Φ₀=f|È_i=1^mt_i, Φ₁(A)dHE₄-X and Φ_t|AÇB=f|AÇB, t0[0, 1]. We now extend Φ to all of D²HI by defining Φ_t|B=f|B, for each t0[0, 1]. Let r be a 2-simplex of È_i=1^mt_i, then Φ|r is a map from (r, Mr) to (H₃, H₄-X). By applying the special case, we see that Φ is homotopic (rel AÇB) in HE₂ to a map G:D²àHE₂-X. Thus f is homotopic (rel B, implying rel MD²) to G in HE₂, and p is 2-connected.

We have, from Stallings' Engulfing Theorem, an ambient isotopy e²:HE₂H[0, 1]àH₂ and a compact set EdHE₂ such that Lde₁²(e'₁(HE₂-X)) and e_t²|(HE₂-E)È(HE₂ÇR²-L)=1|(HE₂-E)È(HE₂ÇR²-L), so that we may extend e_t² by the identity on M-HE₂.

Now define K to be the complex H₂ÇR²de₁²(e'₁(HE₂-X)). Let J be the complementary complex of K in H₂ and let N* be a quasi-cell in HE₁ with JdNE*. As in the proof of Theorem 3.9, let e³:MH[0, 1]àM be an ambient isotopy, fixed outside of H₁, which engulfs e₁²(e'₁(X)) with e₁³(NE*). Define N to be [(e'₁)^-1B(e₁²)^-1Be₁³](N*). €

Prior to proving the third of the theorems about strong quasi-cellularity, we give the definition of a property used in the second of Rushing's infinite engulfing theorems. This property is used to reduce the ULC conditions.

4.6 DEFINITION. Let M be a PL n-manifold, U an open subset of M, and P a PL subspace of dimension k in M. We say that most of P can be pulled through M into U by a short homotopy H:(P-A)HIàM, where cl(A) is a compact subset of P, if
    (1) H(p, 0)=p, for all p0P-A,
    (2) H(p, 1) is in U, for all p0P-A, and
    (3) given e>0, there is a compact set BdP such that DIAM(H(pH[0, 1]))<e, for p0P-B.

4.7 THEOREM. Let M be a PL n-manifold, n$5, and let X be a subset of ME which tends to M-X. Suppose that for each open neighborhood U of X there is an open neighborhood V of X lying in U such that V is ULC^6-n, V-X is ULC^5-n, and for each locally finite triangulation R of M, most of the 2-skeleton R²ÇV can be pulled through V into V-X by a short homotopy. Then X is strongly quasi-cellular if and only if X is closed, has SUV⁴ and satisfies the strong quasi-cellularity criterion.

Proof. Repeat the proof of Theorem 4.5, replacing the use of the first of Rushing's infinite engulfing theorems with the second (5.5, below). €

4.8 REMARK. If n$7 in Theorem 4.7 then the ULC conditions disappear. The resulting theorem is very much like Theorem 3.9. The 0-ULC at X condition for M is replaced by the short homotopy condition. It is possible that the short homotopy can be obtained from SUV⁴ and strong quasi-cellularity in somewhat the same manner as the homotopy pulling locally finite 2-complexes into M-X in U is obtained in Lemma 3.8. However, some other condition, such as 0-ULC at X may be required.

We now state and prove three theorems for sufficiency conditions for weak quasi-cellularity.

4.9 THEOREM. Let M be a PL n-manifold, n$6, and let X be a closed, connected subset of ME such that M is 0-ULC at X and X tends to M-X. Then X is weakly quasi-cellular if X satisfies the weak quasi-cellularity criterion.

Proof. By the definition of the weak quasi-cellularity criterion (2.10), there exists a quasi-special sequence {H_i-1,T_i,Fⁱ}_i=1⁴ for X in M having the null-homotopy property. Then the proof of sufficiency in Theorem 3.9 gives a quasi-cell N with XdNEdNdHE₀dME.

We need only show that for each quasi-cell Q containing X in its interior, there is a sequence of quasi-cells {Q_i}_i=1⁴ lying in Q with XdQE_i+1dQ_i+1dQE_i and X=Ç_i=1⁴Q_i. Since we already have the existence of the quasi-cell N, this will complete the proof.

Write M as the union of a countable number of compact PL n-manifolds, M₁dME₂dM₂dME₃d ... dÈ_i=1⁴M_i=M. Let {e_i}_i=1⁴ be a decreasing sequence of positive numbers converging to zero.

There exists a quasi-special sequence for X in Q having the null-homotopy property, so we may choose Q₁dQE as N was chosen for M. Inductively, suppose Q_j has been defined. Let {H_i-1,T_i,Fⁱ}_i=1⁴ be a quasi-special sequence for X in Q_j with the null-homotopy property. Let H_i have large enough subscript so that H_iÇM_jdN(X;e_j), and as before, there exists a quasi-cell Q_j+1 containing X in its interior with Q_j+1dHE_i. Let {Q_i}_i=1⁴ be the sequence of quasi-cells so defined.

It is clear that XdQE_i+1dQ_i+1dQE_i, for all i. Let p be a point in M-X, and let e=DIST(p, X). Let e_i<e and M_j be such that p0M_j. Then p is not in Q_i+j. Thus X=Ç_i=1⁴Q_i, and the proof is complete. €

4.10 THEOREM. Let M be a PL n-manifold, n$5, and let X be a closed, connected subset of ME which tends to M-X. Suppose that for each open neighborhood U of X there is an open neighborhood V of X lying in U such that V is ULC² and V-X is ULC¹. Then X is weakly quasi-cellular if X satisfies the weak quasi-cellularity criterion.

Proof. Let {H_i-1,T_i,Fⁱ}_i=1⁴ be a quasi-special sequence for X in M having the null-homotopy property. The proof of sufficiency in Theorem 4.5 gives a quasi-cell N with  XdNEdNdHE₀dME. The argument in the proof of Theorem 4.9 finishes the proof. €

4.11 THEOREM. Let M be a PL n-manifold, n$5, and let X be a closed, connected subset of ME which tends to M-X. Suppose that for each open neighborhood U of X there is an open neighborhood V of X lying in U such that V is ULC^6-n, V-X is ULC^5-n, and for each locally finite triangulation R of M, most of the 2-skeleton R²ÇV can be pulled through V into V-X by a short homotopy. Then X is weakly quasi-cellular if X satisfies the weak quasi-cellularity criterion.

Proof. Repeat the proof of Theorem 4.10, replacing the use of the first of Rushing's infinite engulfing theorems with the second (5.5, below). €

4.12 REMARK. If n$7 in Theorem 4.11, we have a theorem without the ULC conditions, as in Remark 4.8.

It should be noted that some of our results are not as strong as they might be. For instance, the conditions X tends to M-X, V is ULC², and V-X is ULC¹ in Theorems 3.9, 4.5, 4.7, 4.9, 4.10, and 4.11 are conditions on the metric of the ambient manifold M. Since quasi-cellularity is a topological concept, it seems natural to suspect that these are conditions which allow us to prove our results in this particular manner, not necessarily conditions required for proof of these results. Obviously, the theorems can be strengthened by weakening the hypotheses by requiring only that there be an ambient isotopy of the ambient manifold so that the image of X under the ambient isotopy has the required conditions. This is a somewhat clumsy requirement, so it is stated here as a remark, rather than being included in each theorem.

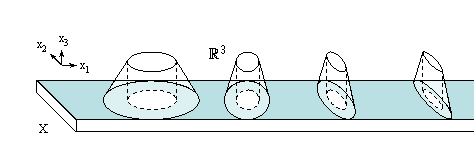
For example, consider X in Figure 1, illustrated in ú³, and its analogs in úⁿ. The bumps have constant height and their indentations have constant depth (x₃-direction) and a constant width (x₂-direction), but have decreasing length (x₁-direction). X does not tend to ú³-X and there is no V that is 0-ULC. If we alternate the bumps with bumps that have decreasing widths, there is no V that is 1-ULC, with V-X either 0-ULC or 1-ULC. Despite these problems, there is an ambient isotopy between either version of X and X' shown in Figure 2. X' does tend to ú³-X and for each closed neighborhood U of X, there is a closed neighborhood V of X in U such that V is ULC² and V-X is ULC⁰. Clearly both X and X' are strongly quasi-cellular, yet only for analogs of X' may we apply any of our results to show this.

Figure 1. Strongly quasi-cellular, but not provable by these theorems

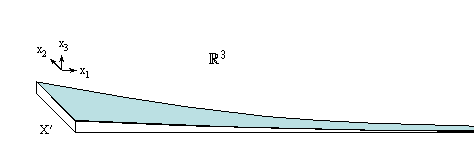
Figure 2. Strongly quasi-cellular, with ambient isotopy to Figure 1

There are other questions that could lead to further research.

For example, the number of ends of a quasi-cell is well-defined and equals the number of ends of a tree of which it is a regular neighborhood. Is the number of ends of a quasi-cell well defined? If so, is there a relation between the number of ends of the defining quasi-cells and the number of ends of the quasi-cellular set? Figures 3 and 4 give examples of strongly quasi-cellular sets and quasi-cells that might appear in sequences used to define the sets. The symbol e_i(Y) refers to the i^th end of Y, for whatever space Y is.

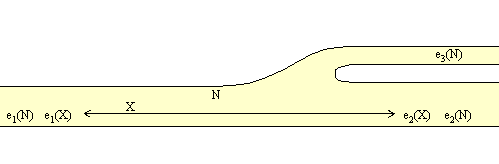
Figure 3. Strongly quasi-cellular set and containing quasi-cell

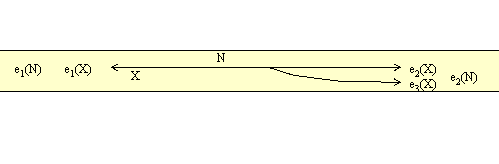
Figure 4. A different strongly quasi-cellular set and containing quasi-cell

A question arises concerning compactification. If a quasi-cellular set is compactified by adding a point at each end, this same compactification of the quasi-cells defining the set gives rise to a "pinched" cell definition of the set. When can these cells be "unpinched" so that the set is cellular? On the other hand, suppose a set is cellular and certain points are removed. If the resulting set and cells minus points are embedded as closed subsets of some manifold, when can quasi-cellularity be achieved? Notice, in Figures 5 and 6, that the cells minus points are neighborhoods of the ends, not necessarily quasi-cells.

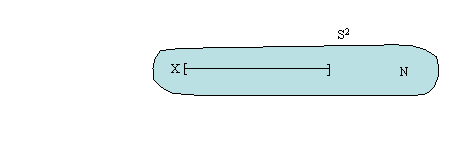
Figure 5. A cellular set and containing cell

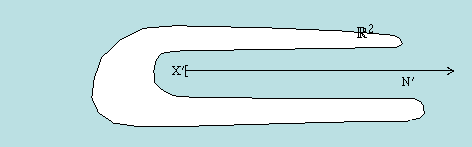
Figure 6. A cellular set minus a point and containing neighborhood

In this example, X is cellular in S² and N is a cell in S² containing X in its interior. Removing an endpoint of X yields X' as a closed subset of ú² and N' as a neighborhood of infinity containing X' in its interior.

5 APPENDIX OF ENGULFING THEOREMS.

Our first engulfing theorem is the Infinite Radial Engulfing Theorem. Bing defines radial engulfing and proves a series of theorems [2]. He also mentions the possibility of infinite engulfing and points out techniques which might be useful [2, Modification 5, p. 7]. Our theorem is a generalization of his radial engulfing in codimension four from section 3 of [2]. We first give a modification of Definition 3.3 which increases the generality of the Infinite Radial Engulfing Theorem in some situations. Our use here of the theorem does not require this generality, however. The proof of our theorem and many ancillary lemmas and definitions are found in [6].

5.1 DEFINITION. Suppose M is a PL n-manifold, U is an open subset of M, and {A_a} is a collection of sets in M. We say locally finite k-complexes in Mⁿ can be pulled into U along {A_a} in M if, for each closed PL subspace P^k of M and closed set QdP^k such that QdU, there is a proper homotopy H:PH[0, 1]àM such that H₀ is the inclusion, H₁(P)dU, H_t is the inclusion on Q, for each p0P, H(pH[0, 1]) lies in an element of {A_a}, and there is a map d:Pà(0, 4) with DIST (H₁(p), M-U)>d(p), for each p0P.

5.2 THEOREM. Suppose U is an open subset of a PL n-manifold M, P is a closed subspace of M, Q is a closed PL subspace of P lying in U and R=cl(P-Q) is r-dimensional, r£n-4. If {A_a} is a collection of subsets of M such that locally finite r-complexes in M can be pulled into U along {A_a}, then for each map e:Rà(0, 4), there exists an engulfing isotopy G:MH[0, 1]àM such that G₀=1, G_t|Q=1|Q, RdG₁(U) and there is a function z:Mà(0, 4), depending on e, such that for each y0M, there exist r+1 or fewer elements of {A_a} such that G(yH[0, 1]) lies in the z(y)-neighborhood of the union of these r+1 elements.

Our next three engulfing theorems are all to be found in Rushing [11]. They are stated for PL manifolds without boundary; however, if a PL manifold has boundary, its interior is a manifold without boundary and the conclusions of these theorems allow for the engulfing isotopies to be extended by the identity on the boundary of such a manifold.

The first of these theorems is Rushing's version of Stallings' Engulfing Theorem.

5.3 THEOREM. Let M be a PL n-manifold without boundary, U an open subset of M, P^k a finite polyhedron in M of dimension k£n-3 and Q^qdU a (possibly infinite) polyhedron of dimension q£n-3 such that (cl(Q)-Q)ÇP=f. Let (M, U) be k-connected. Then there is a compact set EdM and an ambient isotopy e_t of M such that Pde_t(U) and
    e_t|(M-E)ÈQ=1|(M-E)ÈQ.

In the statements of Rushing's Infinite Engulfing Theorems, Mⁿ is a connected PL n-manifold without boundary, U is an open set in M, P^k is an infinite polyhedron of dimension k£n-3, which is contained in M (P is not necessarily closed in M) and Q^q is a (possibly infinite) polyhedron of dimension q£n-3 such that (cl(Q)-Q)ÇP=f and (cl(P)-P)ÇQ=f. The symbol "4^~" denotes a closed subset of M-(PÈQ) containing (cl(P)-P)È(cl(Q)-Q).

Our next theorem appears in [11] as the corollary to the Infinite Engulfing Theorem 1.

5.4 THEOREM. Suppose that M-4^~ is ULC^k, U-4^~ is ULC^k-1 and P tends to U. Then most of P^k can be engulfed by U staying fixed on Q, in the following sense:
    Given a compact set CdP and e>0, there exists and ambient isotopy e_t of Mⁿ such that e_t|(M-N(P-C; e))ÈQ=1|(M-N(P-C; e))ÈQ and such that e₁(U) contains all of P except some compact subset. Furthermore, for each d>0, there exists a compact subset KdM-4^~ such that e_t|M-K is a d-isotopy.

The last theorem is Rushing's Infinite Engulfing Theorem 1 of [11].

5.4 THEOREM. Suppose that M-4^~ is ULC^{max(k,q)+k-n+2}, U-4^~ is ULC^{max(k,q)+k-n+2}. Also suppose that most of P^k can be pulled through M-4^~ into U-4^~ by a short homotopy. Then most of P^k can be engulfed by U in the same sense as in Theorem 5.4

CONTINUATION: "More about Property SUV⁴ and Strong Quasi-Cellularity."

REFERENCES

1. Ball, B. J. and R. B. Sher, "A Theory of Proper Shape for Locally Compact Metric Spaces," Fund. Math., 86 (1974), 164-192.

2. Bing, R. H., "Radial Engulfing," in Conference on the Topology of Manifolds, Prindle, Weber, and Schmidt (Boston), (1968), 1-18.

3. Borsuk, K., "Fundamental Retracts and Extensions of Fundamental Sequences," Fund. Math., 64 (1969), 55-85.

4. Dugundji, J., Topology, Allyn and Bacon, Inc., (Boston), 1966.

5. Hartley, D. S., III, "Fundamentals of Quasi-Cellularity," unpublished.

6. _____________, Quasi-Cellularity in Manifolds, Dissertation, University of Georgia, Athens, GA, 1973 (Ref # A 515428, Dec 27 1973, University Microfilms, 300 North Zeeb Rd, Ann Arbor, MI 48106).

7. Hudson, J. F. P., Piecewise Linear Topology, W. A. Benjamin, Inc., (New York), 1969.

8. McMillan, D. R., Jr., "A Criterion for Cellularity in a Manifold," Ann. of Math. (2) 79(1964), 327-337.

9. ___________, "UV Properties and Related Topics," Mimeographed notes.

10. Mardesic, S., "Retracts in Shape Theory," Glasnik Mat. Ser. III 6 (26), (1971), 153-163.

11. Rushing, T. B., "Infinite Engulfing," preprint. Possibly published as "A summation of results of infinite engulfing," Proceedings of the University of Oklahoma Topology Conference Dedicated to Robert Lee Moore (Norman, Okla., 1972), Univ. of Oklahoma, Norman, Oklahoma, 1972, pp. 284–293.

12. Scott, A., "Infinite Regular Neighborhoods," J. London Math. Soc. 42 (1967), 245-253.

13. Sher, R. B., "Property SUV⁴ and Proper Shape Theory," Trans. Amer. Math. Soc. 190 (1974), 345-356.

14. Spanier, E. H., Algebraic Topology, McGraw-Hill Book Company, (San Francisco), 1966.

15. Stallings, J., "The Piecewise-Linear Structure of Euclidean Space," Proc. Cambridge Philos. Soc. 58 (1962), 481-488.

Return to Website Entrance Page