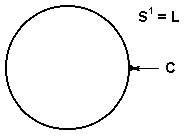
Page Last Updated: Tuesday, 19 January 2016 11:02 EDT, (c) 1973, 2002, 2007, 2008, 2016

PUBS: More about Property SUV⁴ and Strong Quasi-Cellularity

Dean S. Hartley III

Note: If SUV-infinity appears as SUV4, you may not have the font "WP MathA" installed. You may download the WP MathA and WP MathA Extended fonts with control+click on the following links: WPHV06NA.TTF and  WPHV07NA.TTF. (Or you may find them at http://instruct1.cit.cornell.edu/courses/fontfix.htm.) Save the files to your Fonts folder (probably C:\Windows\Fonts). If you cannot save them there, save them somewhere else. Then right click on the file and choose "install." You may have to reboot for these to be applied by Windows.

Abstract. Heretofore the use of property SUV⁴ and strong quasi-cellularity has been restricted to closed subsets of manifolds. These concepts are extended to include non-closed subsets for the purpose of examining the problems: When is the compactification of an SUV⁴ set UV⁴? When is the compactification of a strongly quasi-cellular set cellular? What sets may be removed from a UV⁴ set to obtain an SUV⁴ set? What sets may be removed from a cellular set to obtain a strongly quasi-cellular set? Partial answers are given to these questions.

AMS 1970 Subject Classifications. Primary 57A60, 57C99; Secondary 57C40.
MSC 2000 Subject Classifications. Primary 57N60, 57Q99; Secondary 57Q40, 57Q65.

Key words and phrases. Cellular, cellularity criterion, quasi-cell, quasi-cellular, strongly quasi-cellular, SUV⁴, tree, UV⁴.

NOTATION

UE and Int(U) symbolize the topological interior of U.
ME_i+1 symbolizes the topological interior of M_i+1 (the apparent sequence of the superscript and subscripts is purely an artifact of the HTML).
( €_i)_i=1⁴ symbolizes an operation or group of indexed entities ranging from the index of 1 to the index of 4 (the apparent sequence of the superscript and subscripts is purely an artifact of the HTML).
J⁺ symbolizes the set of positive integers.
ú¹ symbolizes the real number line.
Sⁿ symbolizes the Euclidean n-sphere.
Mⁿ and X^x symbolize n-dimensional and x-dimensional objects, respectively.
Fⁱ and Gⁱ, where F and G are maps, symbolize indexed maps, not n-dimensional objects.
F₀ and F₁, where F is a homotopy, F:XHIàY, symbolize F(X,0) and F(X,1), respectively.
MB symbolizes the boundary of B.
-->> symbolizes an onto map.
Cl(X) symbolizes the topological closure of X.
K symbolizes the complex closure of K.
FY symbolizes the Freudenthal compactification of a space Y.
EY symbolizes the set of ends of Y.
` symbolizes a collapse.

1 INTRODUCTION.

The concepts of SUV⁴ and strong quasi-cellularity were introduced in [3] as extensions of UV⁴ and cellularity to the non-compact case. Further connections among these concepts were also given in [3]. The dissertation [3] was divided into two papers [4 and 5], for publication. In both of these papers, strong quasi-cellularity was defined only for closed subsets of manifolds; and while the definition of property SUV⁴ did not explicitly require that the set in question be closed, in the case that the ambient topological space is a manifold, it was tacitly assumed that the set would be closed. In this paper, we shall examine subsets of manifolds which are not necessarily closed and identify some conditions under which these sets satisfy extended definitions of property SUV⁴ and strong quasi-cellularity. We use some algebraic tools developed by E. M. Brown [2] and R. B. Sher [9], which are still in genesis. As a result, our work is restricted to simplicial complexes in many cases. We also require that all spaces be locally compact metrizable spaces.

2 UV⁴ AND SUV⁴.

2.1 DEFINITION. Suppose Y is a topological space and XdY. Then X is said to have property UV⁴ for each open neighborhood U of X in Y, there is an open neighborhood V of X in U such that V is contractible in U.

We have defined property SUV⁴ in [4] for general topological spaces; however, we shall use a more convenient definition, which is equivalent when the ambient space is a manifold.

2.2 DEFINITION. A tree is a connected, simply connected, locally-finite l-complex.

2.3 DEFINITION. A map f:XàY is proper if f ^-l(C) is compact whenever C is compact.

2.4 DEFINITION. Suppose M is a PL n-manifold n$3, and X is a closed subset of M lying in ME. Then X is said to have property SUV⁴ in M if for each closed neighborhood U of X in M, there is a PL submanifold V, with non-empty boundary, such that XdVEdVdUE, a tree T embedded as a closed PL subset of M lying in UE, and a proper PL homotopy H:VHIàU with H₀ the inclusion, H_l (V)=T and H(VHI)dUE.

It has been shown [8] that property UV⁴ is a property that is topologically invariant with respect to embeddings in metrizable ANRs. It has also been shown [4] that property SUV⁴ is a property which is topologically invariant with respect to embeddings (as a closed subset) in locally compact metric ANRs. The connections between UV⁴ and SUV⁴ are the following: If X0SUV⁴, then X0UV⁴. If X is compact, then X0UV⁴ if and only if X0SUV⁴. There do exist non-compact UV⁴ spaces that are not SUV⁴ (ú² for instance).

From our definition of SUV⁴, it is clear that even if a set X has property SUV⁴ when embedded as a closed subset of a manifold, if it is embedded as a non-closed subset of a manifold, there need not be a submanifold V for each closed neighborhood U such that XdVEdVdUE (cf. [0, 4)dú¹dúⁿ and [0, 1)dú¹dúⁿ). However, the following theorem [9, Theorem 4.3] identifies (in terms of homotopy groups and Brown's proper homotopy groups [2]) those connected locally finite simplicial complexes that may have property SUV⁴. For these spaces, we take the following theorem to be the definition of SUV⁴ for non-closed sets in manifolds.

2.5 THEOREM. Suppose K is a connected locally-finite simplicial complex. Then K0SUV⁴ if and only if

(i) for each n0J⁺, π_n(K)=0, and

(ii) for each n0J⁺c{4} and end [a] of K, π_n(K,a)=0.

2.6 COROLLARY. Suppose L is a compact, connected, locally-finite simplicial complex. Then L0UV⁴, if and only if for each n0J⁺, π_n(L)=0.

We now define the property CCⁿ. This property has been previously defined by Lacher [6] under the name SUVⁿ, which we obviously can't use. We use the "CC" since l-CC is McMillan's cellularity criterion [7], which he names property CC [8].

2.7 DEFINITION. Suppose Y is a topological space and XdY. If for each open neighborhood U of X in Y, there is an open neighborhood V of X in U such that any map f:S^jàV-X can be extended to a map g:B^J+1àU-X, then we say X has property j-CC in Y and write (XdY)0CCⁿ. If X has property j-CC in Y for each 0#j#n, then we say X has property CCⁿ in Y and write (XdY)0CCⁿ. If X has property j-CC in Y for each non-negative integer j, then we say X has property CC^ω in Y. If for each open neighborhood U of X in Y, there is an open neighborhood V of X in U such that V-X is contractible in U-X, then we say X has property CC⁴ in Y.

2.8 THEOREM. If (XdY)0CC⁴, then (XdY)0CC^ω.

We are now in a position to show that certain non-compact subsets of certain compact UV⁴ sets are SUV⁴ sets.

2.9 THEOREM. Suppose L is a compact, connected, locally-finite simplicial complex and L0UV⁴. If C is a compact connected PL subspace of L, K=L-C is connected, C0UV⁴, and (CdL)0CC⁴, then K0SUV⁴.

Proof. We first show that π_n(K)=0, for each N0J⁺. Suppose f:SⁿàK is a map. Then f(Sⁿ)dL and since π_n(L)=0, then f extends to g:Bⁿ⁺¹àL. We may assume that g is a PL map. We use C0UV⁴ and (CdL)0CC⁴ to get n-connectivity by a standard argument [7, 5] and thus homotop g (rel MBⁿ⁺¹) off of C. Hence π_n(K)=0.

We now consider π_n(K,a), for each n0J⁺c{4} and each end [a] of K. Suppose [a] is an end of K, and α:S_nàK is a representative of an element of π_n(K,a), n0J⁺c{4}. Now let U₁=L and V₁dU₁ be chosen using (CdL)0CC⁴ . We write K as an expanding union of compact subcomplexes of a locally finite triangulation of K, K=c_i=1⁴ Q_i, Q_idQE_i+1. Given that j0J⁺ and that V_j has been defined, let Q_k be such that K-V_jdQE_k. Let U_j+1=L-Q_k, and choose V_j+1 using (CdL)0CC⁴. Now for any j0J⁺ only a finite number of images of spheres in Sⁿ are to be found not entirely inside V_j. If we define a homotopy from α to αN, where αN is a map from ([0,4) union a finite number of spheres) to K, by homotoping each sphere in V_j-C (j the largest possible subscript) to a point in U_j-C, then we find this homotopy is proper. Examine the image of the homotopy of any sphere: it is outside some U_j, so that all the spheres inside V_j have homotopies missing the homotopy of the given sphere. Thus only finitely many hit the given sphere's homotopy. Since π_n(K)=0 we may properly homotop αN to a map αNN: [0,4)àK. Since both of these homotopies may be chosen so as to agree on [0,4), α is 0 in π_n(K,a) and so π_n(K,a)=0. Hence K0SUV⁴. €

2.10 COROLLARY. Suppose L is a compact, connected, locally-finite simplicial complex and L0UV⁴. If C is a compact PL subspace of L, K=L-C is connected, and each component of C has UV⁴ and CC⁴ in L, then K0SUV⁴.

The techniques of the proof of Theorem 2.9 can also be used for situations in which LóUV⁴. For instance, we delete the requirement for (CdL)00-CC, and require B_n(L-C)=0 and we can handle such situations as S¹ minus a point, as in Figure 1.

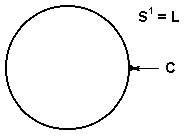
Figure 1. S¹ minus a point.

We now consider the problem in reverse: Suppose K0SUV⁴. If L is a compactification of K, when is L0UV⁴? It is clear that if K has more than one end and L is the one-point compactification of K, then L is not simply connected and thus LóUV⁴. For this reason, we turn to the Freudenthal end point compactification, FK.

2.11 THEOREM. Suppose K0SUV⁴, then L=FK0UV⁴.

Proof. By [9, Theorem 3.1] there is a tree T such that Sh_pK=Sh_pT. Then ShFK=ShFT and, since FT is a compact metric absolute retract, FT0UV⁴. Hence FK0UV⁴. €

3 CELLULARITY AND STRONG QUASI-CELLULARITY.

3.1 DEFINITION. A closed set X lying in the interior of an n-manifold M is said to be cellular in M if there exists a sequence {Ci}_i=1⁴ of n-cells such that MeC₁eCE₁eC₂eCE₂e...e1 _i=1⁴ C_i=X.

3.2 DEFINITION. Suppose N is an n-manifold. If there is a PL n-manifold N¹dEⁿ which is a regular neighborhood of some tree embedded as a closed PL subset of Eⁿ, and if there is a homeomorphism h:N¹-->>N then N is called an n-quasi-cell. If the dimension is obvious, or not relevant, N will be referred to simply as a quasi-cell.

 3.3 DEFINITION. A closed set X lying in the interior of an n-manifold M is said to be strongly quasi-cellular in M if for each closed neighborhood U of X, there is an n-quasi-cell N such that XdNEdNdUE.

We now wish to extend the definition of strong quasi-cellularity. As with SUV⁴ we wish to consider the possibility of X not being a closed subset of the ambient manifold. We also note that when we are dealing with strong quasi-cellularity in the PL category, we mean for the quasi-cells to be PL subspaces.

3.4 DEFINITION. We say that a set X lying in the interior of an n-manifold M is strongly quasi-cellular in M if there is a closed set C lying in the interior of M such that C1X=N, CeCl(X)-X, M-C is an n-manifold and X is strongly quasi-cellular in M-C in the sense of Definition 3.3.

We now are in a position to consider when a compactification of a strongly quasi-cellular set is strongly quasi-cellular and what sets may be removed from a cellular set to yield a strongly quasi-cellular set. In the following theorem, we give a partial answer to the second question.

3.5 THEOREM. Suppose X is a locally-finite simplicial complex embedded as a cellular subset of the PL n-manifold M, n$6. Suppose that C is a closed PL subspace of X, Y=X-C is connected, each component of C has UV⁴ and CC⁴ in X, and M-C is a PL n-manifold. If M-C is 0-ULC at Y, Y tends to M-X and for each closed neighborhood U of Y, there is a closed polyhedral neighborhood V of Y lying in UE such that

(i) the inclusion induced-homeomorphism i_*: π₁(V-X,v)àπ₁(U-X,v) is trivial for all v0V-X, and

(ii) the inclusion-induced homeomorphism π₁(i): π₁(V-X,a)àπ₁(U-X,a) is trivial for all proper maps a:[0,4)àV-C with a([0,4))dV-X, then Y is strongly quasi-cellular in M.

Proof. Since X is cellular, X0UV⁴. By Theorem 2.10, Y0SUV⁴. By [4, Remark 4.21], Y satisfies the strong quasi-cellularity criterion in M-C. Thus Theorem 3.9 of [5] gives us that Y is strongly quasi-cellular in M-C. This satisfies our new definition and Y is strongly quasi-cellular in M. €

The following theorem gives a partial answer to the first question. We use the notation FY for the Freudenthal compactification of a space Y, and EY for the set of ends of Y.

3.6 THEOREM. Suppose X is a closed subset of the PL n-manifold Mⁿ, n$5, such that XdM and X is strongly quasi-cellular in M. Suppose FM is a PL n-manifold, each end of M contains no more than one end of X, and EX1E(MM)=N. Then FX is cellular in FM.

Proof. Since each end of M contains no more than one end of X, and since EX1E(MM)=N, then the construction of FM yields FX as a subset of FM, lying in Int(FM). By [4, Theorem 4.13], X has SUV⁴ in M. By [9, Theorem 3.1], X has the proper shape of a tree. Hence FX has the shape of a point and has UV⁴ in FM.

Suppose U is an open neighborhood of FX in FM. Let U be an open neighborhood of FX in UN that is homotopic to a point in U through a homotopy H. Let N be a quasi-cell neighborhood of X in M1UN. Let EM and EX be the ends of M and X respectively. Since X is closed in M, EXdEM. For each end e in EX, let V_e be a closed polyhedral neighborhood of e in UN such that for e…eN, V_e1V_eN=i. Let l:S₁àInt(Nc(c_eV_e)) be a map. Let NN and VN_e be chosen in a similar manner to N and V_e so that FXdInt(NNc(c_eVN_e)), l(S¹)1(NNc(c_eVN_e))=i, and so that H(l(S¹)HI)1(c_eVN_e)=i. (To achieve this last condition, we must have H(l(S¹)HI)1EX=i. Since EX is a discrete set of points in FM, this may be obtained using general position.) By [4, Lemma 4.8], H may be modified to miss X and thus FX. We now have that FX satisfies the cellularity criterion in FM. Hence, by [7, Theorem 1], FX is cellular in FM. €

We now increase the generality of Theorem 3.6 to include the case for the extended definition of strong quasi-cellularity.

3.7 THEOREM. Suppose X is a subset of the PL n-manifold Mⁿ, n$5, such that XdME and X is strongly quasi-cellular in M. If FM is a PL n-manifold, if the closed set C in Definition 3.4 can be given C=c_i=1^kQ_i, where each Q_i is a flat q_i-cell, 0#q_i#n, Q_i1Q_j=N, for i… j, if each end of M contains no more than one end of XcC, and if E(XcC)1E(MM)=N, then F(XcC) is cellular in FM.

Proof. By the nature of C, there is a homotopy H: MHIàM such that each H_t is a homeomorphism off of C, H₀ is the identity and H₁(Q_i) is a point, for each 1#i#k. Thus H₁(C) is a discrete collection of points. Since applying the Freudenthal compactification to H₁(M-C) with regard to only those ends produced by removing H₁(C) from H₁(M) yields H₁(M) again, then by Theorem 3.6, F(H₁(XcC)) is cellular in F(H₁(M)). From [1, Section 4], we have that each H_t:MàM extends uniquely to a map G_t:(FM,EM)à(F(H_t(M)),E(H_t(M))) with (F(XcC),E(XcC))à(F(H_t(XcC)),E(H_t(XcC))). Since EM=E(H_t(M)) and E(XcC)=E(H_t(XcC)), this family of maps forms a homotopy constant on the ends. Since G_t is a homeomorphism off of F(XcC), by the nature of the cellularity criterion and property UV⁴, then F(H₁(XcC)) having UV⁴ and satisfying the cellularity criterion implies that F(XcC) has UV⁴ and satisfies the cellularity criterion. Again by [7, Theorem 1], F(XcC) is cellular in FM. €

REFERENCES

1. Ball, B. J. and R. B. Sher, "A Theory of Proper Shape for Locally Compact Metric Spaces," Fund. Math., to appear.

2. Brown, E. M., "Proper Homotopy Theory in Simplicial Complexes," preprint. Possibly published as "On the Proper Homotopy Type of Simplicial Complexes," in Topology Conference, LNmaths 375 (1974) Springer, pp 41-46.

3. Hartley, D. S., III, Quasi-Cellularity in Manifolds, Dissertation, University of Georgia, Athens, GA, 1973 (Ref # A 515428, Dec 27 1973, University Microfilms, 300 North Zeeb Rd, Ann Arbor, MI 48106).

4. Hartley, D. S., III, "Fundamentals of Quasi-Cellularity," unpublished.

5. Hartley, D. S., III, "Quasi-Cellularity Criteria," unpublished.

6. Lacher, R. C., "Cell-Like Mappings," I, Pacific J. Math. 30(1969), 717-713.

7. McMillan, D. R., Jr., "A Criterion for Cellularity in a Manifold," Ann. of Math. (2)79(1964), 327-337.

8. McMillan, D. R., Jr., "UV⁴ Properties and Related Topics," Mimeographed notes.

9. Sher, R. B., "Property SUV⁴ and Proper Shape Theory," Trans. Amer. Math. Soc. 190 (1974), 345-356.

Return to Website Entrance Page