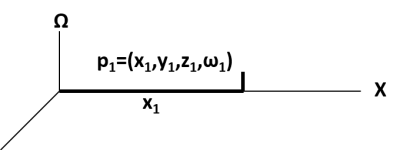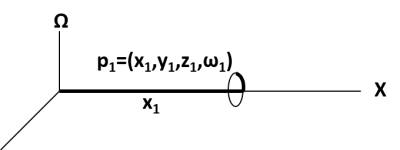Page
Last Updated:
EDT, © 2022, 2024, 2025
|
DEAN
HARTLEY
The Stories, Science,
and Speculative Science in the Dark Energy Series |
-
Dark Energy Series - 6 books: What if telepathy actually exists? How would you prove it? And what if this projective telepathy created positive feedback, enhancing sexual stimuli?
What if you could induce telepathy in others? What would the social implications be?
Robert Adams and Eva Bailey discover that they are telepaths and, as scientists, need to know how telepathy works. They also want to know whether there are other telepaths and if non-telepaths can become telepaths. They expect hostility if the scientific establishment discovers their research too soon, but don’t expect the problems they face from corporate and international sources.
-
Discovery:
[Published July 2025] Telepathy is real - and a problem
Robert Adams and Eva Bailey discover that they are telepaths and, as scientists, need to know how telepathy works. They also want to know whether there are other telepaths and if non-telepaths can become telepaths.
They enlist their friends, Selena, Harold, Dan, and Miriam. After proving to them that their telepathy exists, they test its qualities.
Basically, they can send information, but they cannot pull information from another person: they cannot read minds. However, in certain situations, it dramatically increases sexual stimulation.
As part of their research, they work to determine the speed of transmission, which will yield information about the physics behind the transmissions.
They also work to see if they can find and activate the genes that control telepathy in those without natural telepathy.
They expect hostility if the scientific establishment discovers their research too soon, but don’t expect the problems they face from corporate and international sources.
-
Vindication:
[Published July 2025] Telepathy is real, sexy and lucrative
Robert, Eva and friends have been successful in inducing telepathy in the four friends and in other people.
They have an electronic telepathy detector and have data that suggests that telepathy is faster than light. Just before Robert and Eva got married, a Chinese team had kidnapped Eva.
But with the help of a friendly senator and the FBI, they used the detector to triangulate Eva’s location and the FBI rescued her.
Now, they are working on a series of papers on the biological mechanisms of telepathy and a series on the physics that allows for effective faster-than-light transmission.
They have the basics, but need more data to nail everything down. They also resolve to market the potion that activates telepathy as a sexual enhancer.
As their activities become more public, they receive increased interest from both the Chinese and a commercial espionage firm. Both are convinced that there is technology they can steal.
-
The Swift War:
[Published August 2025] Telepathy is real - and a threat to China
ΨTech, Inc. has partnered with the Oak Ridge National Laboratory and now Robert, Eva, Miriam, Dan, Selena, and Harold are leading interdisciplinary teams from the Lab in discovering more about
telepathy and its faster-than-light physics. They are reveling in doing good science and expanding their sales of telepathy as a sexual enhancer.
And because of their invention of synthetic messages that are secure and travel almost instantaneously from any place on Earth to any other place, they are selling transceivers.
Chinese spies had kidnapped Eva and a European commercial espionage company had burned their office and both had failed to obtain ΨTech’s secrets.
However, the Chinese haven’t given up; they are willing to use military forces to get what they want. The European company hasn’t given up either; they are willing to hire military forces.
-
Gorillas:
[Published August 2025] Telepathic gorillas and Russian aggression
Robert and the other ΨTech partners had thought moving their research to the Oak Ridge National Lab would eliminate the dangers from Chinese and European interests; however, they had been wrong.
Fortunately, both the Chinese and the Europeans had attacked ORNL at the same time and largely wiped out each other’s forces.
After the attack, the US Navy had purchased and installed transceivers in some of its warships. China had attacked the US as a prelude to its invasion of Taiwan.
However, the Navy used its uninterruptible communications with its vessels, including submarines, to wipe out the Chinese navy. With China weakened, Russia and India were seeing an opportunity
and they were thinking about finding telepaths of their own.
Meanwhile, ΨTech investigated telepathy in the great apes, transmissions through the earth using satellites, and blocking unwanted telepathic messages.
-
Society:
[Published September 2025] Telepathy affects societies
Russia and India had invaded China and been repulsed. Russia had failed in its attempt to connect Kaliningrad to the rest of Russia. India had been successful in taking a small part of Kashmir from Pakistan.
China had asked the Taiwanese government to form a temporary government on the mainland and that process had gone well. Therefore, the world was at peace … except that Russia still had ambitions.
And at least five countries were creating telepaths.
Robert and his friends had been involved from time to time in some of these military events; however, most of the time they were working on understanding more about telepathy.
They had discovered that some of the gorillas in the Knoxville Zoo were telepaths and that the others responded to the telepathy inducing treatment. With reliable communications they had started teaching sign language
to the gorillas and were amazed at the intelligence that the gorillas showed.
-
Cultures:
[Published September 2025] Telepathic gorillas discover religion
Robert is investigating the topological structure of the universe and Eva is working on the nature of cognition. Selena is delving into the prediction of volcanic eruptions and Harold is making them all
richer with his transceiver sales. Dan is revolutionizing computing and Miriam is creating a society of gorillas.
Robert, Eva and friends have worked on the origins of language and the necessity for being able to manipulate symbols to be able to think. Without sign language, gorillas hadn’t had a large
set of symbols to manipulate; now they had them. They also discovered that telepathy was increasing the fertility rate for the gorillas, a very good thing for conserving the species.
Pakistan and Russia have had their territorial ambitions squelched. In the meantime, telepathy is affecting the cultures of countries around the world and not uniformly positively.
And the gorillas want to know about God.
-
Sciences used and abused: Physics - ultra-high
energy gamma rays, volcanoes; biology - pineal gland, cognitive processing;
mathematics - information theory, topology; anthropology; sociology;
military science.
|
 
Robert and Eva
 
Selena and Harold
 
Dan & Miriam
Pamela, Jack and young gorilla
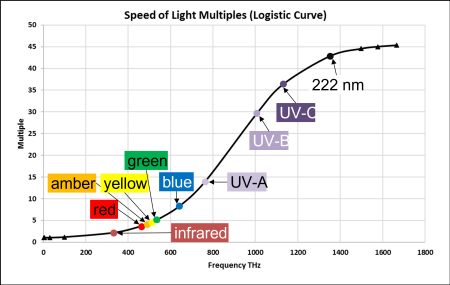
Transmission speeds as a function of frequency
Attack on ORNL by two enemies
 
Tamu
Bishop 'Father Dave' |
Addendum:
These novels are science fiction. That means they are stories with some connection to science, particularly speculative science.
Parapsychology:
We begin with the assumption that psychic abilities or
extrasensory perception (ESP) exists, at least in some people.
There is sufficient anecdotal evidence of various experiences that seem
to be explained best by this assumption to make it a plausible part of a science
fiction tale.
-
Some of the categories of potential psychic abilities
are the following:
-
Telepathy: the ability to transmit or receive thoughts
-
Teleportation: the ability to move objects or the self instantaneously from
one position to another
-
Astral projection: the ability to project the consciousness to a place
separate from the body
-
Levitation: the ability to float or fly by mental power
-
Psychokinesis: the ability to manipulate objects by mental power
-
Clairvoyance: the ability to see persons or events that are distant in time
or space
-
Precognition: the ability to perceive future events
-
Retrocognition: the ability to see past events
-
Remote viewing: the ability to see contemporary events outside the
normal range of perception
Psychic abilities have not been scientifically confirmed
and (at least) two areas of science must be addressed to generate reasonable
explanations. One area is physics:
what physical forces are involved and how do they operate?
For example, must some new particle – say the psychon – be
proposed, perhaps a new boson? The
second area is biology: how does the
biology of a human being interact with the physics?
For example, does it require a previously undiscovered organ?
Some potential psychic abilities present challenges in energetics.
For example, levitation implies the application of energy to raise a body
against the force of gravity. Does
the energy come from the body of the person doing the levitation, as is the case
in climbing stairs? Or does the
person tap into some other source of energy?
We restrict our tale of psychic abilities to those that don’t require
major energy sources to avoid such questions.
There are several organizations devoted to research in this
field.
-
The Society for Psychical Research, headquartered in London, was founded in
1882. It maintains a library,
conducts research and publishes a journal.
Its website is
https://www.spr.ac.uk/.
-
The American Society for Psychical Research, headquartered in New York City,
was founded in 1885 and is the oldest psychic research organization in the
US. It maintains a library and
archives and publishes a journal.
Its website is http://www.aspr.com/.
-
One of the best-known of the psychic research centers is the Rhine Research
Center at Duke University, founded by J.B. Rhine in 1935 as the Duke
Parapsychology Labs. It
maintains a library and publishes a journal.
Its website is
https://www.rhine.org/who-we-are.html.
Each of these organizations can supply information about
what has been discovered about psychic powers through scientific research.
Biology
Our hearing is limited in range and in discriminatory
sensitivity. It is mediated by “hair
cells” in the inner ear that each respond to a particular frequency.
In general, we can distinguish different pitches (sound frequencies);
however, we do classify notes an octave apart (one has double the frequency of
the other) as the “same,” despite hearing the pitch difference.
The average person’s range is spanned by about 10 octaves (20 to 20,000
Hz [cycles per second]), so we hear music in octave cycles.
Elephants and some whales can hear lower pitched sounds and many animals
can hear much higher pitched sounds.
Light also has frequencies. [Wavelength is the inverse of
frequency times the speed of light.
Human vision ranges from about 400 to about 700 nanometers (nm): 4 x 10-7
meters to 7 x 10-7 meters.
This is 7.5 x 1014 Hz to 4.3 x 1014 Hz.
Thus, human vision covers a little less than an octave of the visual
frequencies.] Our color vision is
mediated by three types of cone cells in the eye, each of which responds to a
range of wavelengths. Complex
processing in the brain yields our visualization of the visual spectrum.
Various animals have different numbers of types of cones.
For example, hummingbirds have a fourth cone type that covers the
ultraviolet spectrum (Hotz, 2020).
Smell is mediated by olfactory receptors, which chemically
bind to odorants. The number of
different receptors, together with the fact that odorants can bind to more than
one receptor, permits discrimination among millions of different scents.
The total number of receptors relates to sensitivity.
For example, dogs have about 300 million receptors, while humans have
about 6 million, making dogs much better at detecting scents(Hotz, 2020).
Other senses exist that humans don’t have, such as the
magnetic field sensing of sea turtles (derived from a light-detecting protein),
the electric field sensing of bumblebees, the infrared sensing of pit vipers,
and the accessory olfactory system in most mammals (not humans) and reptiles in
the vomeronasal organ(Hotz, 2020)
(Wikipedia,
2020).
Starting with telepathy, we will not assume some new
particle that must be detected or manipulated in the human body.
Molecular sensing could certainly be a candidate, because the processing
of these molecules is extremely complex, yielding the possibility of large
information transfers; however, the speed of molecular transfers does not match
the needs of telepathy. We see that
sensing of magnetic and electric fields and of the electromagnetic spectrum are
established with biological mechanisms.
The existence of bioluminescence (fireflies, deep-sea fish, etc.)
establishes the biological ability to emit in the electromagnetic spectrum and
the electric eel establishes the ability to create electric fields.
The question of origins and prevalence arises.
Do we postulate a (relatively) new mutation of humans that permits
telepathy or do we postulate an old ability that is generally suppressed in the
genome? We will choose the latter.
Research on the human genome and epigenome supplies a rich field for the
possibility of suppressed genes and the means to activate them by manipulating
the epigenome
(Sinclair
& LaPlante, 2019).
We will assume the ability arose in pre-humans, but proved less useful
than speech. As a matter of
conserving cellular energy, the genes involved were generally suppressed –
though not universally, with some human lines carrying more active genes than
others.
We don’t have an emotional sense, as such.
However, our emotions are connected to our senses.
For instance, the feeling of disgust is rooted in our sense of smell.
When we smell something bad, we feel disgust.
On the other hand, when we feel disgust for something, the pathways in
our brain related to the sense of smell are activated(Stafford, Fleischman, Le Her, &
Hummel, 2018).
Other emotions are similarly connected to our senses, sometimes in
extremely complex ways(Bradbury, 2017).
In this story, we propose that emotions are not directly
communicated telepathically.
However, when a person experiences emotions, these emotions trigger sensory
pathways associated with the emotions.
If the person transmits sensory feelings, they include both the direct
feelings, for instance, of lips against lips, and the emotionally-triggered
associated sensory feelings. The
recipient receives both sets of sensory inputs.
The direct lip feelings merely intensify the feeling of kissing.
However, the emotionally-triggered feelings are interpreted as the
recipients’ own feelings and are registered as indicators of feeling the
associated emotions, intensifying the recipient’s own emotions.
This emotional response is what produces the intense effect of a
passionate kiss. When each party is
sending his or her feelings, the positive feedback of the emotional response
becomes enormously powerful.
Mathematics
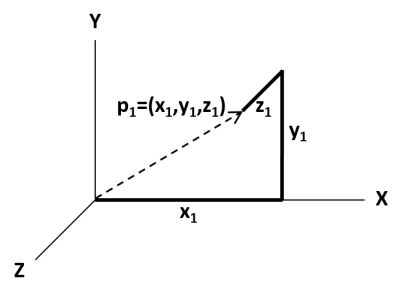
In familiar 3-D space, a point is determined by three
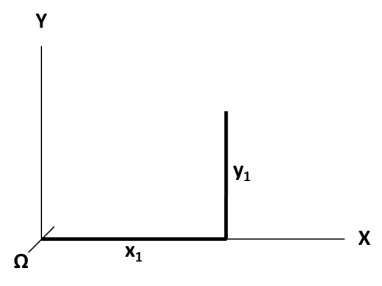
coordinate values, x, y, and z, as shown .
Introducing a Very, Very Small Dimension
Suppose a String Theory is correct and we there exist
around 11 dimensions. Suppose one,
called capital omega (Ω) is microscopic, really small.
the
figure below shows a point with its 3-D
plus Ω coordinates (omitting the Y and Z dimensions in the figure).
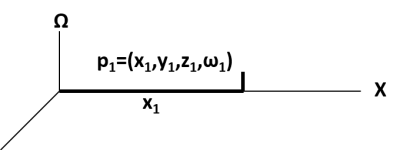
Further, suppose the Ω-dimension is closed into a loop, as
shown .
(For a common example of a closed-loop dimension, see the discussion of
the Mercator Projection Maps in the Mathematics section, below.) In this
illustration, a particle travelling along the X axis can change its omega value,
but not by much. If the total omega
dimension is smaller than a molecule, then a molecule can only vibrate a little
in the omega dimension along its path.
We would not observe this, we would just see the molecule moving along
the X axis.
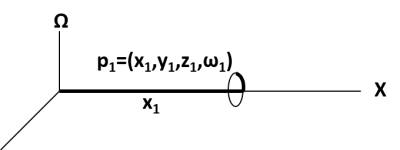
When visualizing just one ordinary dimension (X) and omega,
we see a very long, thin tube (figure below).
A point traveling along any line in the X-Y plane will have its own long,
very thin tube, no matter its direction.
In fact, any path, straight or curved will have its own tube.
This is also true when you consider any path in 3-D space – it will have
its own tube.
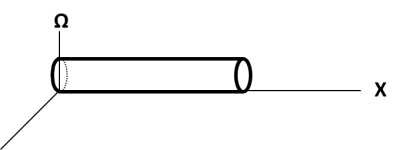
Note that to visualize these tubes, we have added an extra
dimension (besides omega) to indicate the identification of what would have been
the end-points of the short omega dimension.
The identification does not require the extra dimension. It only aids the
visualization. This identification
was used in some of the first computer games in which a rocket ship would travel
to the edge of the screen and reappear on the opposite edge, travelling at the
same angle as it left the screen.
Each point in the X-Y plane also has an Ω extent.
Visualizing this is difficult. One
way of doing this is to substitute Ω for the Z axis, making it very short, as
in the figure below. Then imagine the whole X-Y plane that
intersects the Ω axis at the end closest to you is identified with the whole X-Y
plane at the other end of the Ω axis.
Imagine an airplane flying level at 35,000 feet over a flat
plane with clouds at 70,000 feet. It
is clear for thousands of miles to the front, rear and sides.
The airplane ascends until it hits 70,000 feet, at which point it
reappears at 35,000 feet traveling forward at the same speed as before and
rising at the same rate.
Now substitute a photon for the airplane, X and Y
directions for forward and to the sides and omega for up and down.
35,000 feet represents our normal 3-D space and 52,500 feet represents
the “top” in our tube pictures. The
airplane wings are either the magnetic or electric field sinusoidal curves.
The normal trajectory of a low-energy photon remains at the 35,000-foot
level (zero Ω coordinate). Thus, the
photon travels ‘up’ from 35,000 feet to 52,500 feet; however, when it continues
in that direction it is now traveling ‘down’ in the other half of the loop.
When it has travelled a total of 35,000 feet in that direction, it has
completed circling the loop and arrived back at the 35,000-foot level.
Small compact dimensions such as we have described are not
novel constructs in String theories.
We now propose an additional constraint on Ω.
The portion of the tube that intersects our traditional 3-D space has our
standard distance metric. We could
have the same metric for any line in the X direction on the tube so that the top
line in the illustration has the same length as the bottom line.
However, this is not required.
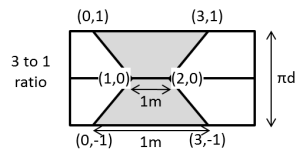
In the
figure below, the middle line shows a
given distance in our 3-D space, say 1 meter.
The larger distance in the join shows that 1 meter extends further on the
top and bottom of the diagram than in the middle – our 3-D space, with the
shaded area showing the rate of change of distances.
(Any curve can be used; straight lines
are easier to draw). We have made
the change yield a three to one ratio, so that the meter in the middle extends
from point (1,0) to point (2,0), where the first coordinate is the X coordinate
and the second coordinate is the Ω coordinate.
On the top, the coordinates for the meter’s ends are (0,1) and (3,1).
On the bottom, they are (0,-1) and (3,-1).
The distance from an Ω coordinate of -1 to +1 is shown as
πd, which we use to
represent the very, very small extent of the Ω-dimension.
(This corresponds to the 35,000-foot length of the airplane-photon loop
above.)
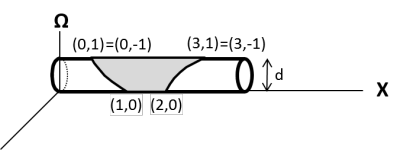
Now, in the figure
below, we identify the bottom
line in igure
above with its top line, rolling
the diagram into a tube, where the joined top and bottom lines appear as the
“top” of the tube. Note that the
“diameter” of the tube is d and we can only see one of the two trapezoids of in this figure.
The result is that a pair of points with the same X coordinates but
different omega coordinates will be closer together at the “top” than at the
“bottom.”
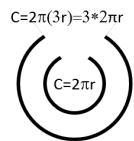
Another way of visualizing this is to consider a lengthwise
cross-section of the tube, embedded in Euclidean 2-space as two circles,
representing a curled tube, as in .span style="mso-spacerun:yes">
The radius of the normal space part of the tube must be equal to 3 times
the radius of the “top” part of the tube.
(The figure actually only has a factor of 2.)
However, the gap between the two must equal the diameter d of the tube –
very, very small. Since the
circumference of the larger circle represents a distance in normal space, these
constraints make it impossible to represent this cross-section as nice circles
for large distances.
Hence, the larger “circle” must be crinkled to show larger
distances. Larger ratios exacerbate
the problem.& .
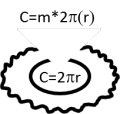
The tube in the figure below shows the crinkled normal
space. The crinkled arrow shows a
photon’s distance traveled in normal space.
The other arrow starts out crinkled and becomes straighter as it travels
further from normal space in the Ω-dimension, indicating a smaller distance
traveled. (For a common example of a
crinkled dimension, see the discussion of the Mercator Projection Maps in the
Mathematics section, below.)
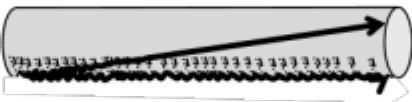
Mercator Projection Maps
The figure below is a Mercator projection map of the
Earth’s surface. Notice that the
left edge of the map is identified with the right edge.
Thus, the main portion of Asia is shown as the large gray continent in
the upper right portion of the figure.
However, the “tail” of Asia appears on the upper left portion of the
figure, to the left of the North American continent.
This identification converts the horizontal dimension of the figure into
a loop and the map into a cylinder.
(Compare this to the looped Ω-dimension
above.)
A second feature of the Mercator projection is the
enlargement of lateral distances at high latitudes.
For example, the coastline of Antarctica is shown as equal to the
circumference of the Earth at the equator.
The actual length of the Antarctic Circle (which would be a line just
above the coastline) is about 9,900 miles and the length of the equator is about
24,900 miles, a factor of 2.5 times larger.
If we were to pinch the top and bottom to account for this (and pinch the
upper half and lower half smoothly, leaving the equator as it is), we would
convert our cylinder into a part of a sphere – a globe with the North Pole and
South Pole cut off. Alternatively,
we could introduce lateral crinkles into the center part of the map to indicate
that there is more distance there than at the top and bottom.
(Compare this to the crinkled X dimension of the figure above.)
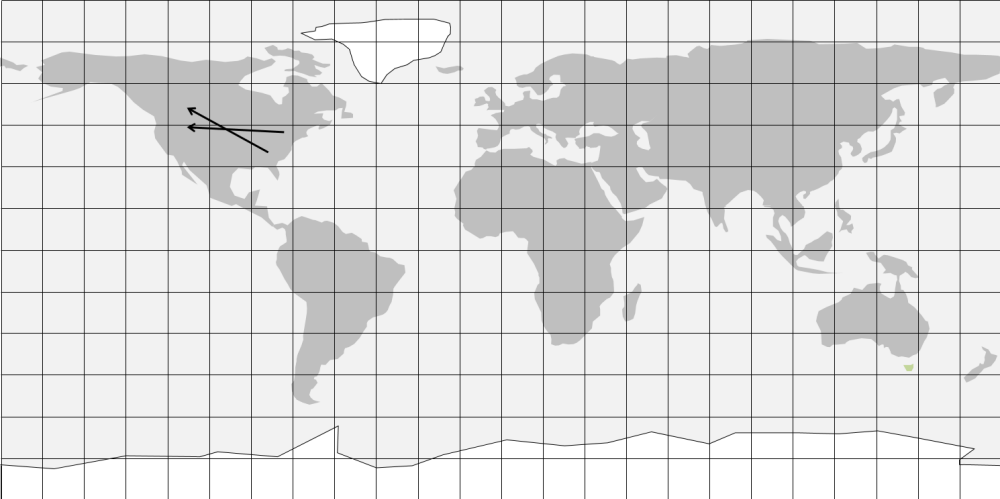
Loxodromers (Rhumb Lines)
A loxodrome (or rhumb line) is a line crossing all
meridians at a constant angle. The
Mercator projection maps of grade-school infamy have a very important property:
lines of constant bearing are straight lines.
That means if you take a compass bearing and travel along that bearing,
you will trace a straight line on a Mercator map.
Alternatively, if you draw a straight course on a Mercator map, you only
have to maintain a constant compass bearing to stay on that course.
However, to convert the course angle shown on the map to a compass
bearing (angle), you have to know the local declination, that is the angle
between the true north pole and the magnetic north pole.
This is because the bearings on the map are based on the clockwise angle
from true north, while the bearings read on a compass are based on the clockwise
angle from magnetic north.
shows a Mercator
projection map of the world and two bearings (shown as arrows) from known points
(the beginning points of the arrows).
To calculate the latitude and longitude of the intersection point is a
simple matter of trigonometry and algebra, once the magnetic bearings are
corrected to be bearings from true north.
Note that while “distances” (from the known points to the intersection)
could be calculated, the “distances” would be in terms of degrees of latitude
and longitude, which have varying values in kilometers or miles.
However, the calculated latitude and longitude of the intersection point
will be correct because the Mercator projection is conformal, preserving angles.
As a practical matter, the smart phone compass app will
give the latitude and longitude of each known point to the second.
The problem lies in determining the correct bearing.
The smart phone app will give a bearing in degrees; however, there will
be an aiming error. This means that
the intersection location will have an error determined by the separation of the
known points and the distance to the intersection.
Determining the exact unknown point within a few meters would require
taking bearings from multiple pairs of points, each new set being successively
closer to the unknown point.
Physics
Gravity
Curved space creates gravity.
The
figure below illustrates the curved
space caused by a massive object, creating a gravity well.
The curvature shown indicates that there is “more space” the closer the
approach to the mass. This extra
space cannot be shown as flat in a 2-D picture; hence the figure shows a dimple
in a third dimension. The dimple
could point up rather than down in an equally valid representation; however, it
points down to fit our feeling that gravity is “down.”

The crinkles inthe
figure before the map also represent “extra
space.” Thus, there is a
gravitational force acting on particles in the tube toward normal space.
Speed of Gamma Rays
The speed of light has been measured very precisely;
however, the speed of x-rays and gamma rays have only been measured at certain
energy levels and with less precision.
If the energy level determines how “high” up into the Ω-dimension the
photon can travel, then the expectation would be for an increase in speed of EM
radiation (such as light) with increasing frequency (which corresponds to
increasing energy). The geometry of
the Ω-dimension would yield a distinctly non-linear relationship.
Thus, conventional x-ray and gamma ray photons would be observed as
having the same velocity as light, within the limits of experimental error.
Only the extremely energetic gamma ray photons of the story, traveling
farther away from normal space in the Ω-dimension would exhibit noticeable
velocities greater than that of light.
Extension of Condensed Matter into the Ω-dimension
Our normal expectation of space-time is that any object has
an extent in each of the three dimensions and the time dimension.
Stated another way, each object is four-dimensional.
The Ω-dimension should be no different.
However, the extent in the Ω-dimension of any condensed matter object
(such as humanly observable objects) should be nearly, but not quite, zero,
since the extent of the Ω-dimension itself is so small.
Here we assume density is one factor that contributes to larger extension
into the Ω-dimension. We will assume
some (very small) fluctuation in a condensed matter particle’s distance away
from normal space, due to thermal vibrations.
Densely packed diamonds (each with high density) are
regarded as one of the best materials to use in detecting high energy gamma
rays. We postulate that certain
diamonds extend sufficiently far into the Ω-dimension to be useful in reacting
to our story’s extremely energetic gamma ray photons.
Penetration of Gamma Rays
Gamma rays are highly penetrative.
They can be attenuated by shielding, with differing materials requiring
differing thicknesses. For example,
the following materials require the given thickness to produce roughly
equivalent shielding:
In our story, we assume that higher energy photons travel
at a greater distance in the Ω-dimension from normal space.
This means they will intersect less condensed matter extending in their
paths, producing greater penetration.
Dark Energy
Dark energy has been proposed as a constituent of the
universe to explain the apparent acceleration of the expansion of the universe.
In this model of the universe, dark energy (which has never been directly
observes) is 68% of the total matter-energy.
In our story, we are assuming a vast sea of
faster-than-light ultra-high energy gamma rays that pervades the universe.
These gamma rays travel in the “upper” part of the Ω-dimension; however,
they do react with normal matter, but only weakly through matter’s small extent
in the Ω-dimension. Their major
interaction is with the topology of the Ω-dimension, pushing against the “lower”
part, causing the expansion of the universe.
Detector Details
The detector described in the book only detects modulated
gamma rays (waves). Gamma rays are
located at the high end of the frequency spectrum of electromagnetic (EM)
radiation, of which visible light and radio waves are small parts.
All EM radiation has a basic form of an oscillating electric field with
an orthogonal oscillating magnetic field.
For simplicity, shows this as a single
sine wave.
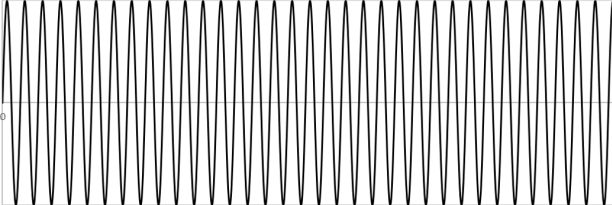
AM (amplitude modulated) radio consists of a basic
frequency EM wave with its amplitude (height in the figure) modulated by a sound
wave – for example, a voice – as illustrated in .
AM frequencies are chosen from a range of 550 to 1720 kHz (thousand
cycles per second). Human hearing
ranges from about 20 to 20,000 Hz (cycles per second).
At an AM frequency of 1000 kHz, a medium pitched sound of 1000 Hz is
about a thousand times slower than the signal to be modulated.
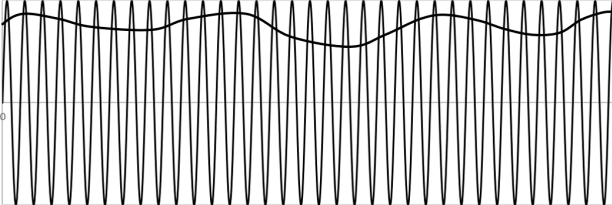
The same principle is used in modulating gamma waves;
however, the frequencies are much larger.
Ultra-high frequency gamma waves have frequencies above 2.8 times 1028
Hz. In the story, these are
modulated with near visible light waves, which range from about 4 to 8 times 1014
Hz. If the basic gamma ray frequency
is chosen to be 4 times 103030 Hz and the modulating light wave is 4
times 1014 Hz, then the frequency multiple is 1016, rather
than 1000 (103) factor for AM radio.
In AM radio reception, the modulated signal is converted to
sound waves. In the gamma ray
detector, only the existence of modulation is detected.
In both cases, the signal strength is a function of the antenna, or
receiving element, particularly involving the direction of the antenna with
respect to the direction of the signal.
When the antenna is properly aligned, the signal is received at maximum
strength. At a 90-degree orientation
to the best alignment, the signal strength is at a minimum, generally zero
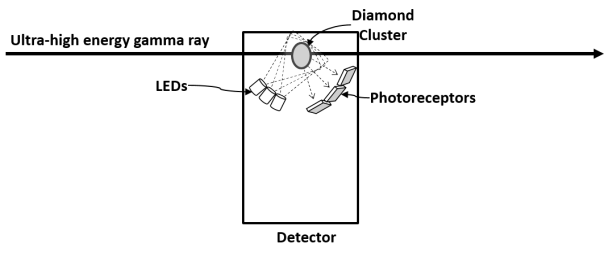
reception. For the gamma ray
detector, the antenna consists of a diamond cluster, bathed in light of
particular frequencies, with that light modified by the diamond cluster and
picked up by a light detector.
illustrates the basic
functioning of the detector. The
LEDs bathe the diamond cluster in near-visible light.
Modulated ultra-high energy gamma rays cause the light bathing the
diamonds to resonate with the gamma rays’ modulation, which is picked up by the
photoreceptors. In the send mode,
the LEDs produce modulated light, which modulates passing ultra-high energy
gamma rays. The chart shows available LEDs, with
their wavelengths in nanometers and frequencies in terahertz.

Biological Connection to Physics
In general, high energy photons
damage living things. We avoid
this problem by considering super-high energy photons, higher-energy than the
gamma rays we can detect. Photons
that we can detect all have insufficient energy to travel much above the level
of normal space because of the enormous gravity field created by very high
values of m (the “crinkle” factor in the math section and hence travel at, or
very slightly above, the speed of light.
Super-high energy photons travel well “above” (in the Ω-dimension) normal
space, travel faster than light, and are not detectable through normal means.
This also means that their extreme ionization capability has no effect on
the human body. However, this
ionization capability makes modulation possible.
We postulate an organ within the brain that responds to
modulation of these super-photons and can induce modulation.
In mystical traditions, this organ has been called the “third eye.”
It is associated with the pineal gland.
Some species of fish, amphibians and reptiles have an actual
photoreceptive third eye, associated with the pineal gland.
“It is absent in mammals, but was present in their closest extinct
relatives, the therapsids
(Wikipedia,
2020).”
We will assume that the genes are retained in humans, but normally
suppressed. New techniques in operating on the genome and epigenome will allow
the re-activation of these genes among those in whom they are suppressed.
We are postulating that this organ grows small, single
crystal diamonds through organic processes similar to the creation of proteins.
In the telepathy reception mode, these diamonds react to modulated
super-high energy photons by producing modulated photons in the visible light
range. These are, in turn, detected
and resolved in the organ and converted by the brain’s processing pathways into
various sensory-type signals. In the
telepathy sending mode, the brain’s sensory signals are converted by a light
emitting portion of the organ, through the diamonds, into modulations of ambient
super-high energy photons. The
detector was designed to mimic this biological design.
In our story, the genes that enable the reception of
telepathy are more frequently activated than are the remainder of the genes that
enable both sending and receiving telepathic messages.
Those with the fully activated gene set create a constant, personalized
“I am here” disturbance that allows a sender to know the direction to send a
message (by selecting gamma rays going in that direction for modulation), rather
than broadcasting it. This “I am
here” signal is not consciously recognizable as is a ‘verbal’ telepathy message.
When sending a message, the sender transmits a “getting ready to send”
signal in the general direction of the intended recipient, who then sends a
precise “ready to receive” signal back, establishing the direct bearing for the
sender to use. These two
connection-establishing signals are also not consciously recognizable.
These three unconsciously received signals are detectable only with the
amber LED, while the conscious messages require the spectrum from amber though
blue for best detection.
Cited Works
Bradbury,
T. (2017, October 25). Emotions: The Sixth Sense. Retrieved September
14, 2020, from Mission.org:
https://medium.com/the-mission/emotions-the-sixth-sense-64fd316961ab#:~:text=They%20allow%20us%20to%20sense,only%20activated%20by%20human%20emotion.&text=De%20Gelder's%20alternate%20pathways%20%E2%80%94%20brain,The%20pathways%20Dr.
Hotz, R. L. (2020, July 13). Different
Wavelengths: Science Fids Hummingbirds See Ultraviolet Light Invisible to
Humans. Retrieved July 30, 2020, from The Wall Street Journal:
https://www.wsj.com/articles/different-wavelengths-science-finds-hummingbirds-see-ultraviolet-light-invisible-to-humans-11594688179
Sinclair, D. A., & LaPlante, M. D. (2019).
Lifespan: Why We Age - and Why We Don't Have To. New York: Atria Books.
Stafford, L. D., Fleischman, D. S., Le Her,
N., & Hummel, T. (2018, February 16). Exploring the Emotion of Disgust:
Differences in Smelling and Feeling. Retrieved September 14, 2020, from
www.mdpi.com: https://www.mdpi.com/2227-9040/6/1/9/pdf
Wikipedia. (2020, July 28). Olfaction.
Retrieved July 30, 2020, from Wikipedia:
https://en.wikipedia.org/wiki/Olfaction
Wikipedia. (2020, June 17). Parietal eye.
Retrieved August 3, 2020, from Wikipedia:
https://en.wikipedia.org/wiki/Parietal_eye
 Return to Dean Hartley Science Fiction
Return to Dean Hartley Science Fiction
 Return to Dr. Dean S. Hartley III Entrance
Return to Dr. Dean S. Hartley III Entrance